
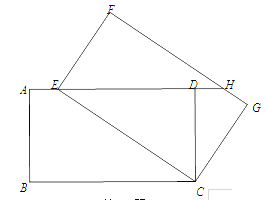
【题目】如图,将矩形ABCD绕点C旋转得到矩形FECG,点E在AD上,延长ED交FG于点H.
(1)求证:△EDC≌△HFE;
(2)连接BE、CH.
①四边形BEHC是怎样的特殊四边形?证明你的结论.
②当AB与BC的比值为 时,四边形BEHC为菱形.
【答案】(1)四边形BEHC为平行四边形,证明见解析;(2)![]()
【解析】试题分析:(1)依据旋转的性质,根据AAS即可证得;(2) ①根据一组对边平行且相等的四边形是平行四边形证得四边形BEHC为平行四边形;②四边形BEHC为菱形,则△BEC是等边三角形,从而∠ABE=30°,即可得到AB与BC的比值.
试题解析:
(1) ∵矩形FECG由矩形ABCD旋转得到,
∴FE=AB=DC,∠F=∠EDC =90°,FH∥EC,∴∠FHE=∠CED,
∴△EDC≌△HFE;
(2) ①
四边形BEHC为平行四边形
∵△EDC≌△HFE,∴EH=EC,
∵矩形FECG由矩形ABCD旋转得到,
∴EH=EC=BC,EH∥BC,
∴四边形BEHC为平行四边形;
②由旋转得BC=CE
∴四边形BEHC是菱形
∴BE=CE
∴BE=BC=CE
∴△BCE是等边三角形
∴∠CBE=60°,
∵四边形ABCD是矩形
∴∠ABC=90°
∴∠ABE=30°
∵cos∠ABE=![]()
∴cos30°=![]()
∴![]()
∴当AB和BC的比值为![]() 时,四边形BEHC为菱形.
时,四边形BEHC为菱形.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点. 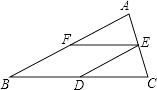
(1)求证:四边形BDEF是菱形;
(2)若AB=12cm,求菱形BDEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市规定:凡一次购买大米180kg以上(含180kg)可以享受折扣价格,否则只能按原价付款.王师傅到该超市买大米,发现自己准备购买的数量只能按原价付款,且需要500元,于是他多买了40kg,就可全部享受折扣价,也只需付款500元.
(1)求王师傅原来准备购买大米的数量x(kg)的范围;
(2)若按原价购买4kg与按折扣价购买5kg大米的付款数相同,那么王师傅原来准备购买多少kg大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知A(0,a),B(b,0),且a、b满足a2﹣4a+20=8b﹣b2 . 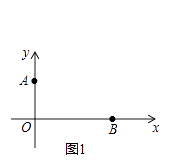
(1)求A、B两点的坐标;
(2)如图2,连接AB,若D(0,﹣6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论; 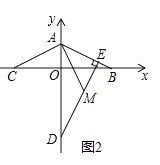
(3)如图3,在(2)的条件下,若N是线段DM上的一个动点,P是MA延长线上的一点,且DN=AP,连接PN交y轴于点Q,过点N作NH⊥y轴于点H,当N点在线段DM上运动时,△MQH的面积是否为定值?若是,请求出这个值;若不是,请说明理由. 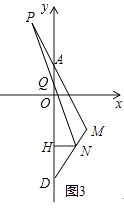
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】23 , 33 , 和43分别可以按如图所示方式“分裂”成2个、3个和4个连续奇数的和.83也能按此规律进行“分裂”,则83“分裂”出的奇数中最大的是 . 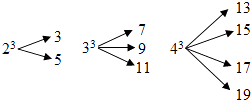
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1 , a2 , a3 , a4…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|…依此类推,则a2017的值为( )
A.﹣1009
B.﹣1008
C.﹣2017
D.﹣2016
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图。 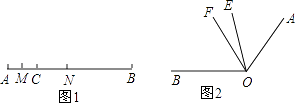
(1)如图1,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
(2)如图2,∠BOE=2∠AOE,OF平分∠AOB,∠EOF=20°.求∠AOB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com