
【题目】如下图。 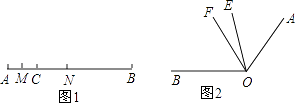
(1)如图1,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
(2)如图2,∠BOE=2∠AOE,OF平分∠AOB,∠EOF=20°.求∠AOB.
【答案】
(1)解:∵M是AC的中点,AC=6,
∴MC= ![]() AC=6×
AC=6× ![]() =3,
=3,
又因为CN:NB=1:2,BC=15,
∴CN=15× ![]() =5,
=5,
∴MN=MC+CN=3+5=8,
∴MN的长为8 cm
(2)解:∵∠BOE=2∠AOE,∠AOB=∠BOE+∠AOE,
∴∠BOE= ![]() ∠AOB,
∠AOB,
∵OF平分∠AOB,
∴∠BOF= ![]() ∠AOB,
∠AOB,
∴∠EOF=∠BOE﹣∠BOF= ![]() ∠AOF,
∠AOF,
∵∠EOF=20°,
∴∠AOB=120°
【解析】(1)直接利用两点之间距离分别得出CN,MC的长进而得出答案;(2)直接利用角平分线的性质以及结合已知角的关系求出答案.
【考点精析】利用两点间的距离和角的平分线对题目进行判断即可得到答案,需要熟知同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记;从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
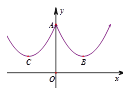
【题目】如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
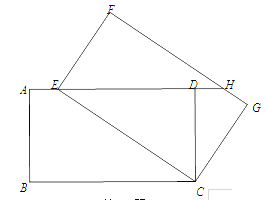
【题目】如图,将矩形ABCD绕点C旋转得到矩形FECG,点E在AD上,延长ED交FG于点H.
(1)求证:△EDC≌△HFE;
(2)连接BE、CH.
①四边形BEHC是怎样的特殊四边形?证明你的结论.
②当AB与BC的比值为 时,四边形BEHC为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划修建一座既是中心对称图形,又是轴对称图形的花坛,从学生中征集到的设计方案有正三角形、正五边形、等腰梯形、菱形等四种图案,你认为符合条件的是
A.正三角形 B.正五边形 C.等腰梯形 D.菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程x2﹣2x﹣3=0经过配方法化为(x+a)2=b的形式,正确的是( )
A. (x﹣1)2=4B. (x+1)4C. (x﹣1)2=16D. (x+1)2=16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个数的和为10,其中一个数为x,那么表示这两个数的积的代数式是( )
A. 10x B. x(10+x) C. x(10-x) D. x(x-10)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com