
【题目】一辆汽车匀速通过某段公路,所需时间![]() 与行驶速度
与行驶速度![]() (km/h)满足函数表达式
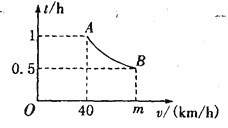
(km/h)满足函数表达式![]() .其图像为如图所示的一段曲线,且端点为A(40,1)和B(
.其图像为如图所示的一段曲线,且端点为A(40,1)和B(![]() ,0.5)
,0.5)
(1)求k和m的值。
(2)若行驶速度不能超过60 km/h,则汽车通过该路段最少需要多长时间?
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名管理人员,对甲、乙两名竞聘者进行了两项测试,各项测试成绩如下表:
测试项目 | 测试成绩(分) | |
甲 | 乙 | |
笔试 | 75 | 84 |
面试 | 88 | 72 |
公司将笔试、面试两项测试成绩分别以60%、40%记入个人最后成绩,并根据成绩择优录用,你认为谁将被录用?(要求写出计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
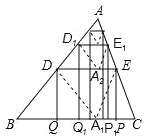
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,折痕与AC边交于点E,分别过点D、E作BC的垂线,垂足为Q、P,称为第1次操作,记四边形DEPQ的面积为S1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,折痕与AC边交于点E1,分别过点D1、E1作BC的垂线,垂足为Q1、P1,称为第2次操作,记四边形D1E1P1Q1的面积为S2;按上述方法不断操作下去…,若△ABC的面积为1,则Sn的值为( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD的对角线AC和BD相交于点O,设有下列条件:①AB=AD;②∠DAB=90°;③AO=CO,BO=DO;④矩形ABCD;⑤菱形ABCD,⑥正方形ABCD,则下列推理不成立的是( )
A. ①④⑥ B. ①③⑤
C. ①②⑥ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.
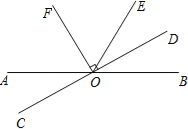
(1)若∠AOE=120°,求∠BOD的度数;
(2)写出图中所有与∠AOD互补的角: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点C将线段AB分成两部分,如果![]() ,那么称点C为线段AB的黄金分割点。某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果
,那么称点C为线段AB的黄金分割点。某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果![]() ,那么称直线l为该图形的黄金分割线。
,那么称直线l为该图形的黄金分割线。
(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点(如图2),则直线CD是△ABC的黄金分割线。你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点C任作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,连接EF(如图3),则直线EF也是△ABC的黄金分割线。请说明理由。
(4)如图4,点E是平行四边形ABCD的边AB的黄金分割点,过点E作EF∥AD,交DC于点F,显然直线EF是平行四边形ABCD的黄金分割线,请你画一条平行四边形ABCD的黄金分割线,使它不经过平行四边形ABCD各边黄金分割点.

查看答案和解析>>
科目:初中数学 来源: 题型:
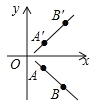
【题目】王杰同学在解决问题“已知A、B两点的坐标为A(3,﹣2)、B(6,﹣5)求直线AB关于x轴的对称直线A′B′的解析式”时,解法如下:先是建立平面直角坐标系(如图),标出A、B两点,并利用轴对称性质求出A′、B′的坐标分别为A′(3,2),B′(6,5);然后设直线A′B′的解析式为y=kx+b(k≠0),并将A′(3,2)、B′(6,5)代入y=kx+b中,得方程组:![]() ,解得
,解得![]() ,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( )
,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( )
A.分类讨论与转化思想 B.分类讨论与方程思想
C.数形结合与整体思想 D.数形结合与方程思想
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com