
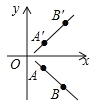
【题目】王杰同学在解决问题“已知A、B两点的坐标为A(3,﹣2)、B(6,﹣5)求直线AB关于x轴的对称直线A′B′的解析式”时,解法如下:先是建立平面直角坐标系(如图),标出A、B两点,并利用轴对称性质求出A′、B′的坐标分别为A′(3,2),B′(6,5);然后设直线A′B′的解析式为y=kx+b(k≠0),并将A′(3,2)、B′(6,5)代入y=kx+b中,得方程组:![]() ,解得
,解得![]() ,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( )
,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( )
A.分类讨论与转化思想 B.分类讨论与方程思想
C.数形结合与整体思想 D.数形结合与方程思想
科目:初中数学 来源: 题型:
【题目】已知一个多项式与3x2+9x的和等于3x2+4x-1,则这个多项式是( )
A. -5x-1 B. 5x+1 C. -13x-1 D. 13x+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车匀速通过某段公路,所需时间![]() 与行驶速度
与行驶速度![]() (km/h)满足函数表达式
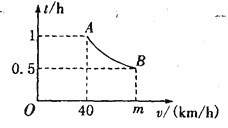
(km/h)满足函数表达式![]() .其图像为如图所示的一段曲线,且端点为A(40,1)和B(
.其图像为如图所示的一段曲线,且端点为A(40,1)和B(![]() ,0.5)
,0.5)
(1)求k和m的值。
(2)若行驶速度不能超过60 km/h,则汽车通过该路段最少需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:①有理数与数轴上的点一一对应;②直角三角形的两边长是5和12,则第三边
长是13;③近似数1.5万精确到十分位;④无理数是无限小数.其中错误说法的个数有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com