练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列语句正确的是（　　）

    A. 1+a不是一个代数式 B. 0是代数式

    C. S=πr2是一个代数式 D. 单独一个字母a不是代数式

    【答案】B

    【解析】

    根据代数式的概念，代数式是用运算符号把数和字母连接而成的式子，即可判断．

    A、1+a是一个代数式，故本选项不符合题意；
    B、0是代数式，故本选项符合题意；
    C、S=πr2是等式，不是一个代数式，故本选项不符合题意；
    D、单独一个字母a是代数式，故本选项不符合题意．
    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】正方体的每一面不同的颜色，对应着不同的数字，将四个这样的正方体如图拼成一个水平放置的长方体，那么长方体的下底面数字和为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一个多边形的内角和与它的外角和相等，则这个多边形是（ ）
    A.三角形
    B.四边形
    C.五边形
    D.六边形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB、CD相交于点O，OF平分∠AOE，OF⊥CD，垂足为O．

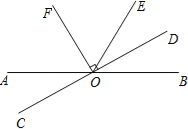
    （1）若∠AOE=120°，求∠BOD的度数；

    （2）写出图中所有与∠AOD互补的角： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点C将线段AB分成两部分，如果，那么称点C为线段AB的黄金分割点。某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1，S2，如果，那么称直线l为该图形的黄金分割线。

    （1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点（如图2），则直线CD是△ABC的黄金分割线。你认为对吗？为什么？

    （2）请你说明：三角形的中线是否也是该三角形的黄金分割线？

    （3）研究小组在进一步探究中发现：过点C任作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF（如图3），则直线EF也是△ABC的黄金分割线。请说明理由。

    （4）如图4，点E是平行四边形ABCD的边AB的黄金分割点，过点E作EF∥AD，交DC于点F，显然直线EF是平行四边形ABCD的黄金分割线，请你画一条平行四边形ABCD的黄金分割线，使它不经过平行四边形ABCD各边黄金分割点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法错误的是（　　）

    A. 平行四边形的内角和与外角和相等

    B. 一组邻边相等的平行四边形是菱形

    C. 对角线互相平分且相等的四边形是矩形

    D. 四条边都相等的四边形是正方形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

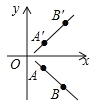
    【题目】王杰同学在解决问题“已知A、B两点的坐标为A（3，﹣2）、B（6，﹣5）求直线AB关于x轴的对称直线A′B′的解析式”时，解法如下：先是建立平面直角坐标系（如图），标出A、B两点，并利用轴对称性质求出A′、B′的坐标分别为A′（3，2），B′（6，5）；然后设直线A′B′的解析式为y=kx+b（k≠0），并将A′（3，2）、B′（6，5）代入y=kx+b中，得方程组：，解得，最后求得直线A′B′的解析式为y=x﹣1．则在解题过程中他运用到的数学思想是（ ）

    A．分类讨论与转化思想 B．分类讨论与方程思想

    C．数形结合与整体思想 D．数形结合与方程思想

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某自行车厂为了赶速度，一周计划生产1400辆自行车，平均每天生产200辆，由于各种原因实际每天生产辆与计划量相比有出入，下表是某周的生产情况（超产为正，减产为负）：

    星期

    一

    二

    三

    四

    五

    六

    日

    增减

    +5

    ﹣2

    ﹣4

    +13

    ﹣10

    +16

    ﹣9

    （1）根据记录可知第一天生产多少辆？

    （2）产量最多的一天比产量最少的一天多生产多少辆？

    （3）赶进度期间该厂实行计件工资加浮动工资制度，即：每生产一辆车的工资为60元，超过计划完成任务每辆车则在原来60元工资上在奖励15元；比计划每少生产一辆则在应得的总工资上扣发15元（工资按日统计，每周汇总一次），求该厂工人这一周的工资总额是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列语句中，正确的是（）

    A. 长度相等的两条弧是等弧 B. 相等的圆周角所对的弧相等

    C. 相等的弧所对的圆心角相等 D. 平分弦的直径垂直于弦

    查看答案和解析>>

    同步练习册答案