
ΓΨΧβΡΩΓΩ»γΆΦΘ§RtΓςABC÷–Θ§ΓœACB=90ΓψΘ§AC=6cmΘ§BC=8cmΘ§Ε·ΒψP¥”ΒψB≥ωΖΔΘ§‘ΎBA±Ώ…œ“‘ΟΩΟκ5cmΒΡΥΌΕ»œρΒψA‘»ΥΌ‘ΥΕ·Θ§Ά§ ±Ε·ΒψQ¥”ΒψC≥ωΖΔΘ§‘ΎCB±Ώ…œ“‘ΟΩΟκ4cmΒΡΥΌΕ»œρΒψB‘»ΥΌ‘ΥΕ·Θ§‘ΥΕ· ±ΦδΈΣtΟκΘ®0ΘΦtΘΦ2Θ©Θ§Ν§Ϋ”PQΘ°

Θ®1Θ©»τΓςBPQ”κΓςABCœύΥΤΘ§«σtΒΡ÷ΒΘΜ
Θ®2Θ©Ν§Ϋ”AQΘ§CPΘ§»τAQΓΆCPΘ§«σtΒΡ÷ΒΘΜ
Θ®3Θ© ‘÷ΛΟςΘΚPQΒΡ÷–Βψ‘ΎΓςABCΒΡ“ΜΧθ÷–ΈΜœΏ…œΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©t=1Μρ![]() ±Θ§ΓςBPQ”κΓςABCœύΥΤΘΜΘ®2Θ©t=
±Θ§ΓςBPQ”κΓςABCœύΥΤΘΜΘ®2Θ©t=![]() ΘΜΘ®3Θ©÷ΛΟςΦϊΫβΈω.
ΘΜΘ®3Θ©÷ΛΟςΦϊΫβΈω.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΘΚΔΌΒ±ΓςBPQΓΉΓςBAC ±Θ§ ![]() Θ§Β±ΓςBPQΓΉΓςBCA ±Θ§
Θ§Β±ΓςBPQΓΉΓςBCA ±Θ§ ![]() Θ§‘ΌΗυΨίBP=5tΘ§QC=4tΘ§AB=10cmΘ§BC=8cmΘ§¥ζ»κΦΤΥψΦ¥Ω…ΘΜ
Θ§‘ΌΗυΨίBP=5tΘ§QC=4tΘ§AB=10cmΘ§BC=8cmΘ§¥ζ»κΦΤΥψΦ¥Ω…ΘΜ
Θ®2Θ©ΙΐPΉςPMΓΆBC”ΎΒψMΘ§AQΘ§CPΫΜ”ΎΒψNΘ§‘ρ”–PB=5tΘ§PM=3tΘ§MC=8-4tΘ§ΗυΨίΓςACQΓΉΓςCMPΘ§ΒΟ≥ω![]() Θ§¥ζ»κΦΤΥψΦ¥Ω…ΘΜ
Θ§¥ζ»κΦΤΥψΦ¥Ω…ΘΜ
Θ®3Θ©ΉςPEΓΆAC”ΎΒψEΘ§DFΓΆAC”ΎΒψFΘ§œ»ΒΟ≥ωDF=![]() Θ§‘ΌΑ―QC=4tΘ§PE=8-CM=8-4t¥ζ»κ«σ≥ωDFΘ§ΙΐBCΒΡ÷–ΒψRΉς÷±œΏΤΫ––”ΎACΘ§ΒΟ≥ωRC=DFΘ§D‘ΎΙΐRΒΡ÷–ΈΜœΏ…œΘ§¥”Εχ÷Λ≥ωPQΒΡ÷–Βψ‘ΎΓςABCΒΡ“ΜΧθ÷–ΈΜœΏ…œΘ°
Θ§‘ΌΑ―QC=4tΘ§PE=8-CM=8-4t¥ζ»κ«σ≥ωDFΘ§ΙΐBCΒΡ÷–ΒψRΉς÷±œΏΤΫ––”ΎACΘ§ΒΟ≥ωRC=DFΘ§D‘ΎΙΐRΒΡ÷–ΈΜœΏ…œΘ§¥”Εχ÷Λ≥ωPQΒΡ÷–Βψ‘ΎΓςABCΒΡ“ΜΧθ÷–ΈΜœΏ…œΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏAC=6cmΘ§BC=8cmΘ§
ΓύAB=![]() =10cmΘ§
=10cmȧ
ΔΌΒ±ΓςBPQΓΉΓςBAC ±Θ§
ÿ![]() ȧBP=5tȧQC=4tȧAB=10cmȧBC=8cmȧ
ȧBP=5tȧQC=4tȧAB=10cmȧBC=8cmȧ
Γύ![]() Θ§
Θ§
Γύt=1ΘΜ
ΔΎΒ±ΓςBPQΓΉΓςBCA ±Θ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύt=![]() Θ§
Θ§
Γύt=1Μρ![]() ±Θ§ΓςBPQ”κΓςABCœύΥΤΘΜ
±Θ§ΓςBPQ”κΓςABCœύΥΤΘΜ
Θ®2Θ©»γΆΦΥυ ΨΘ§ΙΐPΉςPMΓΆBC”ΎΒψMΘ§AQΘ§CPΫΜ”ΎΒψNΘ§‘ρ”–PB=5tΘ§PM=PBsinB=3tΘ§BM=4tΘ§MC=8-4tΘ§
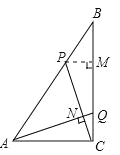
ΓΏΓœNAC+ΓœNCA=90ΓψΘ§ΓœPCM+ΓœNCA=90ΓψΘ§
ΓύΓœNAC=ΓœPCM«“ΓœACQ=ΓœPMC=90ΓψΘ§
ΓύΓςACQΓΉΓςCMPΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΫβΒΟΘΚt=![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦΘ§ΉςPMΓΆBC”ΎΒψMΘ§PQΒΡ÷–Βψ…ηΈΣDΒψΘ§‘ΌΉςPEΓΆAC”ΎΒψEΘ§DFΓΆAC”ΎΒψFΘ§
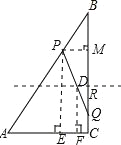
ΓΏΓœACB=90ΓψΘ§
ΓύDFΈΣΧί–ΈPECQΒΡ÷–ΈΜœΏΘ§
ΓύDF=![]() Θ§
Θ§
ÿQC=4tȧPE=8-BM=8-4tȧ
ΓύDF=![]() =4Θ§
=4Θ§
ΓΏBC=8Θ§ΙΐBCΒΡ÷–ΒψRΉς÷±œΏΤΫ––”ΎACΘ§
ΓύRC=DF=4≥…ΝΔΘ§
ΓύD‘ΎΙΐRΒΡ÷–ΈΜœΏ…œΘ§
ΓύPQΒΡ÷–Βψ‘ΎΓςABCΒΡ“ΜΧθ÷–ΈΜœΏ…œΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§ΓœB=60ΓψΘ§ΒψD «BC±Ώ…œΒΡΒψΘ§CD=1Θ§ΫΪΓςABC―Ί÷±œΏADΖ≠’έΘ§ ΙΒψC¬δ‘ΎAB±Ώ…œΒΡΒψE¥ΠΘ§»τΒψP «÷±œΏAD…œΒΡΕ·ΒψΘ§‘ρΓςPEBΒΡ÷ή≥ΛΒΡΉν–Γ÷Β « Θ°
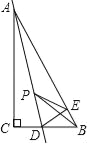
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ’ΐ±»άΐΚ· ΐy=Θ®k+2Θ©xΘ§»τyΒΡ÷ΒΥφxΒΡ÷ΒΒΡ‘ω¥σΕχΦθ–ΓΘ§‘ρkΒΡ÷ΒΩ…Ρή «Θ®ΓΓΓΓΘ©
A. 0B. 2C. -4D. -2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΤΥψΘΚΘ®6x4©¹8x3Θ©Γ¬Θ®©¹2x2Θ©©¹Θ®3x+2Θ©Θ®1©¹xΘ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΓΔ±ϊ»ΐΈΜ―Γ ÷Ης10¥Έ…δΜς≥…Φ®ΒΡΤΫΨυ ΐΚΆΖΫ≤νΆ≥ΦΤ»γ±μΘΚ
―Γ ÷ | ΦΉ | ““ | ±ϊ |
ΤΫΨυ ΐ | 9.3 | 9.3 | 9.3 |
ΖΫ≤ν | 0.026 | a | 0.032 |
“―÷Σ““ «≥…Φ®ΉνΈ»Ε®ΒΡ―Γ ÷Θ§«“““ΒΡ10¥Έ…δΜς≥…Φ®≤ΜΕΦ“Μ―υΘ§‘ρaΒΡ÷ΒΩ…Ρή «Θ®ΓΓΓΓΘ©
A. 0B. 0.020C. 0.030D. 0.035
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςAOB «÷±Ϋ«»ΐΫ«–ΈΘ§ΓœAOB=90ΓψΘ§OB=2OAΘ§ΒψA‘ΎΖ¥±»άΐΚ· ΐy=![]() ΒΡΆΦœσ…œΘ°»τΒψB‘ΎΖ¥±»άΐΚ· ΐy=
ΒΡΆΦœσ…œΘ°»τΒψB‘ΎΖ¥±»άΐΚ· ΐy=![]() ΒΡΆΦœσ…œΘ§‘ρkΒΡ÷ΒΈΣΘ® Θ©
ΒΡΆΦœσ…œΘ§‘ρkΒΡ÷ΒΈΣΘ® Θ©

AΘ°-4 BΘ°4 CΘ°-2 DΘ°2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΒψD «BCΒΡ÷–ΒψΘ§ΒψEΘ§FΖ÷±π‘ΎœΏΕΈADΦΑΤδ―”≥ΛœΏ…œΘ§«“DE=DFΘ°Ηχ≥ωœ¬Ν–ΧθΦΰΘΚ

ΔΌBEΓΆECΘΜΔΎBFΓΈCEΘΜΔέAB=ACΘΜ
¥”÷–―Γ‘ώ“ΜΗωΧθΦΰ ΙΥΡ±Ώ–ΈBECF «Νβ–ΈΘ§Ρψ»œΈΣ’βΗωΧθΦΰ « Θ®÷ΜΧν–¥–ρΚ≈Θ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ABΖ÷±π «Γ―OΒΡ÷±ΨΕΘ§AC «œ“Θ§DC «Γ―OΒΡ«–œΏΘ§CΈΣ«–ΒψΘ§ADΓΆDC”ΎΒψDΘ°
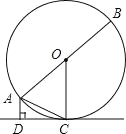
Θ®1Θ©“―÷ΣΓœACD=aΘ§«σΓœAOCΒΡ¥σ–ΓΘΜ
Θ®2Θ©«σ÷ΛΘΚAC2=ABΓΛADΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com