
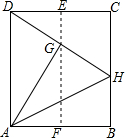
 如图,在一张长方形纸片ABCD中,AD=25cm,AB=20cm,点E,F分别是CD和AB的中点.现将这张纸片按图示方式折叠,求∠DAH的大小及EG的长(精确到0.1cm).
如图,在一张长方形纸片ABCD中,AD=25cm,AB=20cm,点E,F分别是CD和AB的中点.现将这张纸片按图示方式折叠,求∠DAH的大小及EG的长(精确到0.1cm). 分析 由翻折的性质可知:AH=AD=25cm.在Rt△ABH中,由勾股定理可求得BH=15cm,于是得到tan∠HAB=$\frac{HB}{AB}$=$\frac{3}{4}$,从而可知∠HAB≈37°,于是可求得∠DAH≈53°.由翻折的性质可知:AG=AB=20,AF=$\frac{1}{2}AB=10$.在Rt△AFG中,由勾股定理可求得FG≈17.32cm于是的得到EG≈7.7.
解答 解:由翻折的性质可知:AH=AD=25cm.
在Rt△ABH中,BH=$\sqrt{A{H}^{2}-A{B}^{2}}$=$\sqrt{2{5}^{2}-2{0}^{2}}=15$cm.
∵tan∠HAB=$\frac{HB}{AB}$=$\frac{3}{4}$.
∴∠HAB≈37°
∴∠DAH≈90°-37°=53°.
由翻折的性质可知:AG=AB=20cm,AF=$\frac{1}{2}AB=10$cm.
在Rt△AFG中,FG=$\sqrt{2{0}^{2}-1{0}^{2}}$=10$\sqrt{3}$≈17.32cm.
EG=EF-FG≈25-17.32≈7.7cm.
点评 本题主要考查的是翻折的性质、勾股定理的应用,根据翻折的性质求得AH、AG、AF的长是解题的关键.


科目:初中数学 来源: 题型:解答题
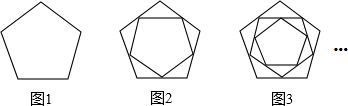
| 图形标号 | 1 | 2 | 3 | … |
| 正五边形个数 | 1 | 2 | 3 | … |
| 三角形个数 | 0 | 5 | 10 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
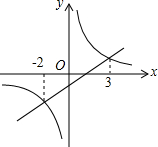 如图,一次函数y1=kx+b图象与反比例函数y2=$\frac{m}{x}$图象的两交点横坐标分别为-2、3,观察图象,写出y1>y2时,x的取值范围是-2<x<0,或x>3.
如图,一次函数y1=kx+b图象与反比例函数y2=$\frac{m}{x}$图象的两交点横坐标分别为-2、3,观察图象,写出y1>y2时,x的取值范围是-2<x<0,或x>3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com