
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
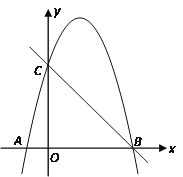
(1)求抛物线的解析式,并直接写出B点的坐标;
(2)已知点![]() 在第一象限的抛物线上,求点
在第一象限的抛物线上,求点![]() 关于直线
关于直线![]() 对称的点的坐标;
对称的点的坐标;
(3)在(2)的条件下,连接![]() ,点
,点![]() 为抛物线上一点,且
为抛物线上一点,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)y=-x2+3x+4.B(4,0);(2)(0,1).(3)(2,6)
【解析】
试题分析:(1)将点A、C的坐标代入抛物线的解析式中,然后解方程组即可.然后令y=0,即可解决问题;
(2)首先由(1)的抛物线解析式确定点D的坐标,此时可以看出CD平行于x轴,由于OB=OC,即△OCB是等腰直角三角形,所以∠OCB=∠DCB=45°,因此点D关于直线BC的对称点恰好在y轴上,将点C向下平移CD长个单位就能求出这个对称点的坐标.
(3)利用待定系数法先求出直线BC的解析式,然后过点P作y轴的平行线,交直线BC于点Q,用未知数设出点P、Q的坐标,即可得到线段PQ的长度表达式,以PQ为底、OB为高,即可得到△PBC的面积函数关系式,根据函数的性质即可求出△PBC的面积最大时,点P的坐标.
试题解析:(1)依题意,有:
![]() ,解得
,解得![]()
∴抛物线的解析式:y=-x2+3x+4.
令y=0,则-x2+3x+4=0
解得:x1=-1,x2=4
故B(4,0);
(2)将点D(m,m+1)代入y=-x2+3x+4中,得:
-m2+3m+4=m+1,化简,得:m2-2m-3=0
解得:m1=-1(舍),m2=3;
∴D(3,4),因此CD∥x轴;
由B(4,0)、C(0,4)可得:OB=OC=4,即△OBC是等腰直角三角形,得:
∠OCB=∠DCB=45°;
设点D关于直线BC的对称点为点E,则点E在y轴上,且CD=CE=3,OE=OC-CE=1,则:
点D关于直线BC的对称点的坐标为(0,1).
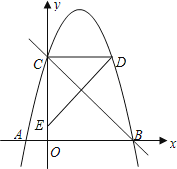
(3)由B(4,0)、C(0,4)可知,直线BC:y=-x+4;
过点P作PQ∥y轴,交直线BC于Q,
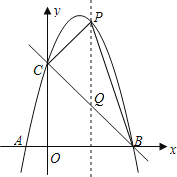
设P(x,-x2+3x+4),则Q(x,-x+4);
∴PQ=(-x2+3x+4)-(-x+4)=-x2+4x;
S△PCB=![]() PQ×OB=
PQ×OB=![]() ×(-x2+4x)×4=-2(x-2)2+8;
×(-x2+4x)×4=-2(x-2)2+8;
所以,当P(2,6)时,△PCB的面积最大.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某校随机抽査了8名参加2019年成都市初中学业水平考试学生的体育成绩,得到的结果如下表:
成绩(分) | 46 | 48 | 49 | 50 |
人数(人) | 1 | 1 | 2 | 4 |
则这8名同学的体育成绩的众数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子商投产一种新型电子产品,每件制造成本为18元,试销过程发现,每月销量y(万件)与销售单价x(元)之间关系可以近似地看作一次函数![]() .
.
(1)写出每月的利润z(万元)与销售单价x(元)之间函数解析式(利润=售价-制造成本);
(2)当销售单价为多少元时,厂商每月能够获得350万元的利润?当销售单价为多少元时,厂商每月能够获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题(不写作法,保留作图痕迹):
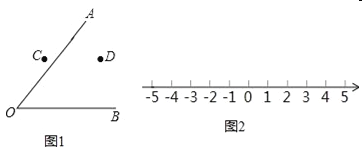
(1)尺规作图:校园有两条路OA、OB,在交叉路口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置P(如图1).(不写画图过程,保留作图痕迹)
(2)用直尺和圆规在如图2所示的数轴上作出表示![]() 的点.
的点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com