
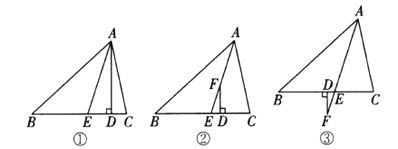
【题目】在![]() 中,
中,![]() .如图①,
.如图①,![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,则易知
,则易知![]() .
.
(1)如图②,![]() 平分
平分![]() ,
, ![]() 为
为![]() 上的一点,且
上的一点,且![]() 于点
于点![]() ,这时
,这时![]() 与
与![]() 、
、![]() 有何数量关系?请说明理由;
有何数量关系?请说明理由;
(2)如图③,![]() 平分
平分![]() ,
,![]() 为
为![]() 延长线上的一点,
延长线上的一点,![]() 于点
于点![]() ,请你写出这时
,请你写出这时![]() 与
与![]() 、
、![]() 之间的数量关系(只写结论,不必说明理由).
之间的数量关系(只写结论,不必说明理由).
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由角平分线的性质和三角形的内角和得出∠BAE=90°-![]() (∠C+∠B),外角的性质得出∠AEC=90°+
(∠C+∠B),外角的性质得出∠AEC=90°+![]() (∠B-∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(∠B-∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(2)由角平分线的性质和三角形的内角和得出∠BAE=90°-![]() (∠C+∠B), 外角的性质得出∠DEF=90°+
(∠C+∠B), 外角的性质得出∠DEF=90°+![]() (∠B-∠C), 在△EFD中,由三角形内角和定理可得∠EFD;
(∠B-∠C), 在△EFD中,由三角形内角和定理可得∠EFD;
试题解析:
∠EFD=![]() (∠C-∠B),理由如下:
(∠C-∠B),理由如下:
∵AE平分∠BAC,
∴∠BAE=![]() =90°-
=90°-![]() (∠C+∠B),
(∠C+∠B),
∵∠AEC为△ABE的外角,
∴∠AEC=∠B+90°-![]() (∠C+∠B)=90°+
(∠C+∠B)=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C)
(∠B-∠C)
∴∠EFD=![]() (∠C-∠B).
(∠C-∠B).
(2)∠EFD=![]() (∠C-∠B),理由如下:
(∠C-∠B),理由如下:
∵AE平分∠BAC,
∴∠BAE=![]() .
.
∵∠DEF为△ABE的外角,
∴∠DEF=∠B+![]() =90°+
=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C),
(∠B-∠C),
∴∠EFD=![]() (∠C-∠B).
(∠C-∠B).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
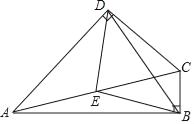
【题目】如图,B、D、C三点在一条直线上,∠ADB=∠ADC=90°,BD=DE,∠DAC=45°;
(1)线段AB、CE的关系为 ;
(2)若BD=a,AD=b,AB=c,请利用此图的面积式证明勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点.(1)求证:△BED是等腰三角形:
(2)当∠BCD=_____°时,△BED是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【新知理解】
如图①,若点![]() 、
、![]() 在直线l同侧,在直线l上找一点
在直线l同侧,在直线l上找一点![]() ,使
,使![]() 的值最小.
的值最小.
作法:作点![]() 关于直线l的对称点
关于直线l的对称点![]() ,连接
,连接![]() 交直线l于点
交直线l于点![]() ,则点
,则点![]() 即为所求.
即为所求.
【解决问题】
如图②,![]() 是边长为6cm的等边三角形
是边长为6cm的等边三角形![]() 的中线,点
的中线,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,则
上,则![]() 的最小值为 cm;
的最小值为 cm;
【拓展研究】
如图③,在四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() .(保留作图痕迹,并对作图方法进行说明)
.(保留作图痕迹,并对作图方法进行说明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】游泳池常需进行换水清洗,图中的折线表示的是游泳池换水清洗过程“排水—清洗—灌水”中水量y(m3)与时间t(min)之间的函数图象.
(1)根据图中提供的信息,求整个换水清洗过程水量y(m3)与时间t(min)的函数表达式;
(2)问排水、清洗、灌水各花多少时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD的边AB=3,AD=2,将此矩形置入直角坐标系中,使AB在x 轴上,点C 在直线y=x-2上.
(1)求矩形各顶点坐标;
(2)若直线y=x-2与y轴交于点E,抛物线过E、A、B三点,求抛物线的关系式;
(3)判断上述抛物线的顶点是否落在矩形ABCD内部,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com