
【题目】游泳池常需进行换水清洗,图中的折线表示的是游泳池换水清洗过程“排水—清洗—灌水”中水量y(m3)与时间t(min)之间的函数图象.
(1)根据图中提供的信息,求整个换水清洗过程水量y(m3)与时间t(min)的函数表达式;
(2)问排水、清洗、灌水各花多少时间?

【答案】(1)答案见解析;(2) 答案见解析
【解析】解:(1)排水阶段:设解析式为:y=kt+b,
图象经过(0,1500),(25,1000),则:
![]()
解得:k=-20,b=1500,
故排水阶段解析式为:y=-20t+1500;
清洗阶段:y=0,
灌水阶段:设解析式为:y=at+c,
图象经过(195,1000),(95,0),则:
![]()
解得:a=10,c=-950,
灌水阶段解析式为:y=10t-950;
(2)∵排水阶段解析式为:y=-20t+1500;
∴y=0时,0=-20t+1500,
解得:t=75,
则排水时间为75分钟,
清洗时间为:95-75=20(分钟),
∵根据图象可以得出游泳池蓄水量为1500(m3),
∴1500=10t-950,
解得:t=245,
故灌水所用时间为:245-95=150(分钟).
答:排水时间为75分钟;清洗时间20分钟;灌水所用时间150分钟.


科目:初中数学 来源: 题型:
【题目】为了节省空间,家里的饭碗一般是摆起来存放的,如果6只饭碗(注:饭碗的大小形状都一样,下同)摆起来的高度为15cm,9只饭碗摆起来的高度为20cm,李老师家的碗橱每格的高度为36cm,则李老师一摞碗最多只能放__只.
查看答案和解析>>
科目:初中数学 来源: 题型:
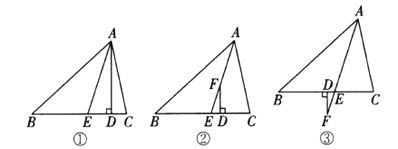
【题目】在![]() 中,
中,![]() .如图①,
.如图①,![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,则易知
,则易知![]() .
.
(1)如图②,![]() 平分
平分![]() ,
, ![]() 为
为![]() 上的一点,且
上的一点,且![]() 于点
于点![]() ,这时
,这时![]() 与
与![]() 、
、![]() 有何数量关系?请说明理由;
有何数量关系?请说明理由;
(2)如图③,![]() 平分
平分![]() ,
,![]() 为
为![]() 延长线上的一点,
延长线上的一点,![]() 于点
于点![]() ,请你写出这时
,请你写出这时![]() 与
与![]() 、
、![]() 之间的数量关系(只写结论,不必说明理由).
之间的数量关系(只写结论,不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在休息天用药薰消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图![]() 所示,点
所示,点![]() 为矩形
为矩形![]() 边
边![]() 的中点,在矩形
的中点,在矩形![]() 的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员
的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路线匀速行进,到达点
的路线匀速行进,到达点![]() .设运动员
.设运动员![]() 的运动时间为
的运动时间为![]() ,到监测点的距离为
,到监测点的距离为![]() .现有
.现有![]() 与
与![]() 的函数关系的图象大致如图
的函数关系的图象大致如图![]() 所示,则这一信息的来源是( ).
所示,则这一信息的来源是( ).


A. 监测点![]() B. 监测点
B. 监测点![]() C. 监测点
C. 监测点![]() D. 监测点
D. 监测点![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产A产品x吨所需费用为P元,而卖出x吨这种产品的售价为每吨Q元, 已知P=![]() x2+5x+1000,Q=-
x2+5x+1000,Q=-![]() +45.
+45.
(1)该厂生产并售出x吨,写出这种产品所获利润W(元)关于x(吨)的函数关系式;
(2)当生产多少吨这种产品,并全部售出时,获利最多?这时获利多少元? 这时每吨的价格又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一条抛物线经过A(0,3),B(4,6)两点,对称轴是x=![]() .
.
(1)求这条抛物线的关系式.
(2)证明:这条抛物线与x轴的两个交点中,必存在点C,使得对x轴上任意点D都有AC+BC≤AD+BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
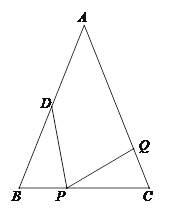
【题目】如图,已知△ABC中,AB=AC=6cm,BC=4cm,点D为AB的中点.
⑴如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CPQ是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为______cm/s时,在某一时刻也能够使△BPD与△CPQ全等.
⑵若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都按逆时针方向沿△ABC的三边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在△ABC的哪条边上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com