
如图,在平面直角坐标系xOy中,直线l⊥y轴于点B(0,﹣2),A为OB的中点,以A为顶点的抛物线y=ax2+c与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
(1)求抛物线的解析式;
(2)若⊙P与y轴的另一交点为E,且OE=2,求点P的坐标;
(3)判断直线l与⊙P的位置关系,并说明理由.
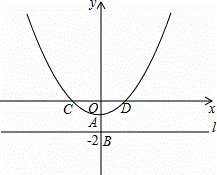
解:(1)∵点A为OB的中点,
∴点A的坐标为(0,﹣1).
∵CD=4,由抛物线的对称性可知:点C(﹣2,0),D(2,0),
将点A(0,﹣1),C(﹣2,0),D(2,0)代入抛物线的解析式得: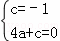 ,
,
解得: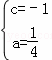 ,
,
∴抛物线得解析式为y=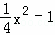 .
.
(2)如下图:过点P1作P1F⊥OE.
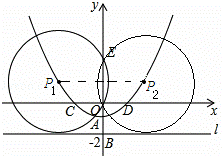
∵OE=2,
∴点E的坐标为(0,2).
∵P1F⊥OE.
∴EF=OF.
∴点P1的纵坐标为1.
同理点P2的纵坐标为1.
将y=1代入抛物线的解析式得:x1=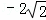 ,x2=2
,x2=2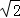 .
.
∴点P1(﹣2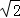 ,1),P2(﹣2
,1),P2(﹣2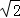 ,1).
,1).
如下图:
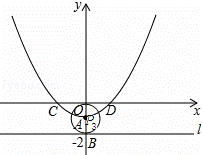
当点E与点B重合时,点P3与点A重合,
∴点P3的坐标为(0,﹣1).
综上所述点P的坐标为(﹣2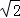 ,1)或(2
,1)或(2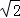 ,1)或(0,﹣1).
,1)或(0,﹣1).
(3)设点P的坐标为(m,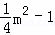 ),
),
∴圆的半径OP=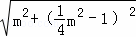 =
=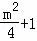 ,
,
点P到直线l的距离=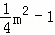 ﹣(﹣2)=
﹣(﹣2)=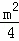 +1.
+1.
∴d=r.
∴直线l与圆P相切.


科目:初中数学 来源: 题型:
“魅力凉都六盘水”某周连续7天的最高气温(单位°C)是26,24,23,18,22,22,25,则这组数据的中位数是( )
A.18 B.22  C.23 D.24
C.23 D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天 桥,市政部门决定降低坡度,使新坡面DC的坡度为i=
桥,市政部门决定降低坡度,使新坡面DC的坡度为i= :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: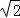 ≈1.414,
≈1.414,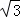 ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
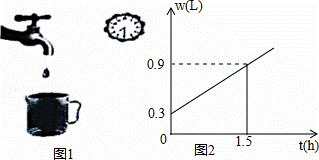
水龙头关闭不严会造成滴水,容器内盛水时w(L)与滴水时间t(h)的关系用可以显示水量的容器做如图1的试验,并根据试验数据绘制出如图2的函数图象,结合图象解答下列问题.
(1)容器内原有水多少升?
(2)求w与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com