
【题目】如图所示,已知C是∠AOB的平分线上一点,点P,P′分别在边OA,OB上,如果要得到OP=OP′,需要添加以下条件中的某一个,那么所有可能结果的序号为________.
①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.
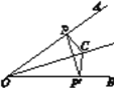
【答案】①②④
【解析】
由射线OC上的任意一点到∠AOB的两边的距离都相等,根据角平分线的判定定理可知OC平分∠AOB .要得到OP=O P′,就要让△OCP≌△OCP′,①②④都行,只有③PC=P′C 不行,因为证明三角形全等没有边边角定理.
①若①∠OCP=∠OCP′,根据ASA定理可求出△OCP≌△OCP′,由三角形全等的性质可知OP=O P′.正确;
②若∠OPC=∠OP′C,根据AAS定理可得△OCP≌△OCP′,由三角形全等的性质可知OP=O P′.正确;
③若PC=P′C 条件不能得出.错误;
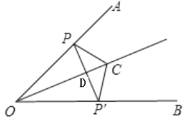
④若PP′⊥OC ,根据ASA定理可求出△OPD≌△![]() ,由三角形全等的性质可知OP=O P′.正确.
,由三角形全等的性质可知OP=O P′.正确.
故答案为①②④.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,现将一张矩形ABCD的纸片一角折叠,若能使点D落在AB边上F处,折痕为CE,恰好∠AEF=60°,延长EF交CB的延长线于点G. 
(1)求证:△CEG是等边三角形;
(2)若矩形的一边AD=3,求另一边AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若四边形ABCD、四边形GFED都是正方形,AD=4, ![]() ,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 .
,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:
时间分组(小时) | 频数(人数) | 频率 |
0≤t<0.5 | 10 | 0.2 |
0.5≤t<1 | 0.4 | |
1≤t<1.5 | 10 | 0.2 |
1.5≤t<2 | 0.1 | |
2≤t<2.5 | 5 | |
合计 | 1 |
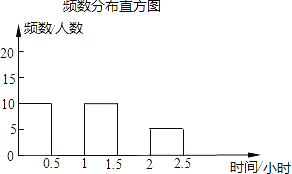
请你将频数分布表和频数分布直方图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是 ![]() ;
;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
A.①②③
B.②③④
C.②③
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
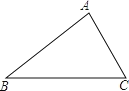
【题目】如图,△ABC中,∠A=84°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到AC、BC两边的距离也相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ABP=15°,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完“证明(二)”一章后,老师布置了一道思考题:如图,点M、N分别在正三角形ABC的边BC.CA上,且BM=CN,AM、BN交于点Q。求证:∠BQM=60°。
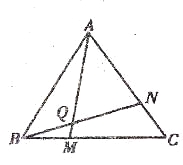
(1)请你完成这道思考题;
(2)做完(1)后,同学们在老师的启发下进行了反思,提出了许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60°?
③若将题中的条件“点M,N分别在正三角形ABC的BC、CA边上”改为“点M,N分别在正方形ABCD的BC,CD边上”,是否仍能得到∠BQM=60°?对②,③进行证明。(自己画出对应的图形)
查看答案和解析>>
科目:初中数学 来源: 题型:
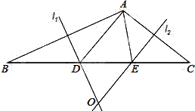
【题目】如图,在△ABC中,AB边的垂直平分线![]() 交BC于D,AC边的垂直平分线
交BC于D,AC边的垂直平分线![]() 交BC于E,
交BC于E, ![]() 与
与![]() 相交于点O,△ADE的周长为6cm.
相交于点O,△ADE的周长为6cm.
(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O是△ABC的外接圆, ![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.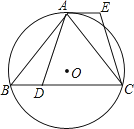
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com