
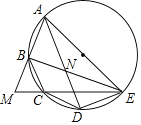
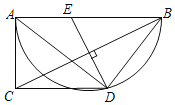
【题目】如图,圆的内接五边形ABCDE中,AD和BE交于点N,AB和EC的延长线交于点M,CD∥BE,BC∥AD,BM=BC=1,点D是![]() 的中点.
的中点.
(1)求证:BC=DE;
(2)求证:AE是圆的直径;
(3)求圆的面积.
【答案】(1)证明见解析;(2)证明见解析;(3)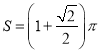 .
.
【解析】
(1)根据平行线得出∠DCE=∠CEB,求出![]() 即可;
即可;
(2)求出AB=BC=BM,得出△ACB和△BCM是等腰三角形,求出∠ACE=90°即可;
(3)根据![]() 求出∠BEA=∠DAE=22.5°,∠BAN=45°,求出BN=1,
求出∠BEA=∠DAE=22.5°,∠BAN=45°,求出BN=1,![]() ,根据勾股定理求出AE2的值,即可求出答案.
,根据勾股定理求出AE2的值,即可求出答案.
(1)证明:∵CD∥BE,
∴∠DCE=∠CEB,
∴![]() ,
,
∴DE=BC;
(2)证明:连接AC,
∵BC∥AD,
∴∠CAD=∠BCA,
∴![]() ,
,
∴AB=DC,
∵点D是![]() 的中点,
的中点,
∴![]() ,
,
∴CD=DE,
∴AB=BC.
又∵BM=BC,
∴AB=BC=BM,即△ACB和△BCM是等腰三角形,
在△ACM中,![]() ,
,
∴∠ACE=90°,
∴AE是圆的直径;

(3)解:由(1)(2)得:![]() ,
,
又∵AE是圆的直径,
∴∠BEA=∠DAE=22.5°,∠BAN=45°,
∴NA=NE,
∴∠BNA=∠BAN=45°,∠ABN=90°,
∴AB=BN,
∵AB=BM=1,
∴BN=1,
∴![]() .
.
由勾股定理得:AE2=AB2+BE2=![]() ,
,
∴圆的面积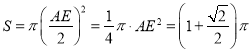 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
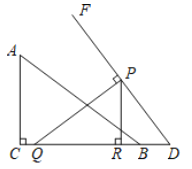
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() .在
.在![]() 上方作射线
上方作射线![]() ,使
,使![]() .点
.点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度,沿射线
出发,以每秒1个单位长度的速度,沿射线![]() 方向运动.过点
方向运动.过点![]() 作
作![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交线段
,交线段![]() 或线段
或线段![]() 于点
于点![]() ,当点
,当点![]() 与点
与点![]() 重合时,点
重合时,点![]() 停止运动.设点
停止运动.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)线段![]() 的长为______.(用含
的长为______.(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值.
的值.
(3)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当点![]() 在
在![]() 的某一条边的中垂线上时,直接写出
的某一条边的中垂线上时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善教室空气环境,某校九年级1班班委会计划到朝阳花卉基地购买绿植.已知该基地一盆绿萝与一盆吊兰的价格之和是12元.班委会决定用60元购买绿萝,用90元购买吊兰,所购绿萝数量正好是吊兰数量的两倍.
(1)分别求出每盆绿萝和每盆吊兰的价格;
(2)该校九年级所有班级准备一起到该基地购买绿萝和吊兰共计90盆,其中绿萝数量不超过吊兰数量的一半,该基地特地对吊兰价格给出了如下的优惠政策,一次性购买的吊兰超过20盆时,超过部分的吊兰每盆的价格打8折,根据该基地的优惠信息,九年级购买这两种绿植各多少盆时总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚![]() 处测得一座建筑物顶点
处测得一座建筑物顶点![]() 的仰角为
的仰角为![]() ,沿山坡向上走到
,沿山坡向上走到![]() 处再测得该建筑物顶点
处再测得该建筑物顶点![]() 的仰角为
的仰角为![]() .已知
.已知![]() 米,
米,![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,山坡坡度为
,山坡坡度为![]() (即
(即![]() ).注:取
).注:取![]() 为
为![]() .
.
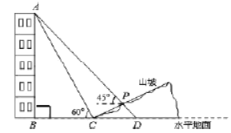
(1)求该建筑物的高度(即![]() 的长).
的长).
(2)求此人所在位置点![]() 的铅直高度(测倾器的高度忽略不计).
的铅直高度(测倾器的高度忽略不计).
(3)若某一时刻,![]() 米长木棒竖放时,在太阳光线下的水平影长是
米长木棒竖放时,在太阳光线下的水平影长是![]() 米,则同一时刻该座建筑物顶点
米,则同一时刻该座建筑物顶点![]() 投影与山坡上点
投影与山坡上点![]() 重合,求点
重合,求点![]() 到该座建筑物的水平距离.
到该座建筑物的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆的直径,点D在半圆弧上,过点D作AB的平行线与过点A半圆的切线交于点C,点E在AB上,若DE垂直平分BC,则![]() =______.
=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下面的两位数18, 27,36, 45,54,63,72,81,99都是9的整数倍,小明发现这些数的个位数字与十位数字的和也都是9的整数倍,例如18的的个位数字8与十位数字1的和是9.于是小明有了这样的结论:个位数字与十位数字的和是9的倍数的两位数一定是9的倍数.小明经过思考后给出了如下的证明:
设十位上的数字为![]() ,个位上的数字为
,个位上的数字为![]() ,并且
,并且![]() (
(![]() 为正整数)
为正整数)
那么这个两位数可表示为![]()
![]()
∴这个两位数是9的倍数
小明猜想:个位数字与十位数字与百位数字的和是9的倍数的三位数也一定是9的倍数.小明的这个猜想的结论是否正确?若正确模仿小明的证明思路给出证明,若不正确举出反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社推出一条成本价为500元/人的省内旅游线路.游客人数![]() (人/月)与旅游报价
(人/月)与旅游报价![]() (元/人)之间的关系为
(元/人)之间的关系为![]() ,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com