
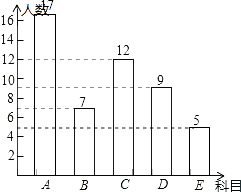
����Ŀ��ijУ���Ż���������ѡ���У�����A��������B��������C������ë��D����ƹ����E����ÿ��ѧ��ѡ�����е�һ�ţ�ѧУ��ij��ȫ��ͬѧ��ѡ��������е���ͳ�ƺ��Ƴ�����������ͳ��ͼ�� 
��1����������ð��������������ȫƵ���ֲ�ֱ��ͼ��
��2���ð������ij4��ͬѧ��1��ѡ������A����2��ѡ������B����1��ѡ������C������Ҫ����4����ѡ2�ˣ��������б�����״ͼ�ķ�������ѡ����2��ǡ��1��ѡ������1��ѡ������ĸ��ʣ�
���𰸡�
��1���⣺������=12��24%=50���ˣ���E������=50��10%=5���ˣ���
����A������=50��7��12��9��5=17���ˣ���
Ƶ���ֲ�ֱ��ͼΪ��
��2���⣺�б����£�
��һ����ѡ�� �ڶ�����ѡ�� | A | B | B | C |
A | AB | AB | AC | |
B | AB | BB | BC | |
B | AB | BB | BC | |
C | AC | BC | BC |
����12�ֵȿ��ܵĽ����������ѡ����2��ǡ��1��ѡ������1��ѡ������Ľ����Ϊ4��
����ѡ����2��ǡ��1��ѡ������1��ѡ������ĸ���= ![]() =
= ![]()
����������1������A���������������ռ�İٷֱȼ��ɵõ����������ټ����E��������Ȼ������A��������ȫƵ���ֲ�ֱ��ͼ����2�������б���չʾ����12�ֵȿ��ܵĽ���������ҳ�ѡ����2��ǡ��1��ѡ������1��ѡ������Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
�����㾫��������Ƶ���ֲ�ֱ��ͼ���б�������״ͼ���ǽ����ĸ�������Ҫ֪���ص㣺��������ʾ�����Ƶ���ֲ��������������ʾ�����Ƶ����𣮣�ע����������ͳ��ͼ��Ƶ���ֲ�ֱ��ͼ������һ������Ҫ�����������������ʱ�����б����Ͳ������ˣ�Ϊ�˲��ز�©���г����п��ܵĽ����ͨ��������״ͼ������ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��AD��BC���ϵ����ߣ���ADΪֱ������O������BO���ӳ�����E��ʹ��OE=OB������O�ڵ�F������AE��CE�� 
��1����֤��AE�ǡ�O�����ߣ�
��2����֤���ı���ADCE�Ǿ��Σ�
��3����BD= ![]() AD=4������Ӱ���ֵ������
AD=4������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С÷�ҵ���̨�Ϸ�����һ��ɹ�¼���ͼ1��ͼ2��ɹ�¼ܵIJ���ʾ��ͼ��A��B�������ڵ��棬��ɹ�¼��ȹ��ſ�������Žǡ�AOB=62�㣬����OA=OB=140cm��С÷������ȹ�����¼ܺ���ܳ���Ϊ122cm���ʽ��������ȹ������ɹ�¼����Ƿ�����䵽���棿��ͨ������˵�����ɣ��ο����ݣ�sin59���0.86��cos59���0.52��tan59���1.66��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ʒ�������һ��ɱ�Ϊ10Ԫ/����С����ƷͶ���г������������������飬�õ��������ݣ� 
���۵���x��Ԫ/���� | �� | 20 | 30 | 40 | 50 | 60 | �� |
ÿ��������y������ | �� | 500 | 400 | 300 | 200 | 100 | �� |
��1�����ϱ���x��y�ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬����y��x�ĺ�����ϵ�������������ϵʽ��
��2�������۵���Ϊ����Ԫʱ������Ʒ��������С����Ʒÿ���õ����������������Ƕ��٣�������=���۶�ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����߾�����A��2��0����B��t��0����t��2������y�ύ�ڵ�C��ֱ��l��y=x+2t������C����x���ڵ�D��ֱ��AE���������ڵ�E�����С�CAE=��CDO����CF��AE�ڵ�F��
��1�����CDO�Ķ�����
��2�������F����ı���ʽ���ú�t�Ĵ���ʽ��ʾ����
��3����S��COD��S�ı���COAF=7ʱ���������߽���ʽ��
��4������B��C��O����Ϊ��������������CEF����ʱ����ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��˫����y= ![]() �ĵ�һ������һ֧�ϣ�AB��ֱ��y���ڵ�B����C��x���������ϣ���OC=2AB����E���߶�AC�ϣ���AE=3EC����DΪOB���е㣬����ADE�����Ϊ3����k��ֵΪ ��
�ĵ�һ������һ֧�ϣ�AB��ֱ��y���ڵ�B����C��x���������ϣ���OC=2AB����E���߶�AC�ϣ���AE=3EC����DΪOB���е㣬����ADE�����Ϊ3����k��ֵΪ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���¶��壺ֱ��l1��l��l2 �� �ཻ�ڵ�O����Ϊm���߶�AB��ֱ��l2�ϣ���P��ֱ��l1��һ�㣬��Q��ֱ��l��һ�㣮����AQB=2��APB�������dzƵ�P�ǵ�Q�İ��µ㣻
��1����ͼ1��ֱ��l2��l�ļн�Ϊ30�㣬�߶�AB�ڵ�O�Ҳ࣬��OA=1��m=2����Ҫʹ�á�APB=45���������P�ǵ�Q�İ��µ㣬��OQ= 
��2����ͼ2����ֱ��l1��l2�ļн�Ϊ60�㣬��m=3����Ҫʹ�á�APB=30�㣬�߶�AB��ֱ��l2�������ƶ���
�ٵ�OA�ij�Ϊ����ʱ�����������İ��µ�P����ֻ��һ������˵�����ɣ�
���Ƿ���ڷ��������İ��µ�P������������������ڣ���ֱ��д��OA�����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����ABΪֱ������O���ֱ�AC��BC�ڵ�D��E�� 
��1����֤��BE=CE��
��2�����BAC=40��ʱ����ADE�Ķ�����
��3������E����O�����ߣ���AB���ӳ����ڵ�F����AO=EF=2ʱ����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧ��ͳ��֪ʶ��С�վͱ���ͬѧ��ѧ��ϲ���ij��з�ʽ��������һ�ε��飮ͼ��1����ͼ��2���������ݲɼ������ݻ��Ƶ�������������ͳ��ͼ�������ͼ���ṩ����Ϣ����������⣺ 
��1����ȫ����ͳ��ͼ������������ﳵ����������Ӧ��Բ�ĽǵĶ�����
��2�����ȫ�꼶��600��ͬѧ�������ȫ�꼶������ѧ��ѧ��������
��3������3����ϲ���˳�����ѧ����1����ϲ�����С���ѧ����1����ϲ���ﳵ����ѧ����Ӳμ�һ����������ѡ��2�˵����鳤���������������г����п��ܵ�����������2�˶��ǡ�ϲ���˳�����ѧ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com