
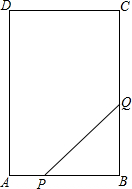
 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB边向点B以1cm/s的速度运动,同时,点Q从点B出发沿BC边向点C以2cm/s的速度运动,P,Q两点在分别到达B,C两点后就停止运动,设经过ts时,△PBQ的面积为S cm2
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB边向点B以1cm/s的速度运动,同时,点Q从点B出发沿BC边向点C以2cm/s的速度运动,P,Q两点在分别到达B,C两点后就停止运动,设经过ts时,△PBQ的面积为S cm2科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到点E,使∠BDE=∠E,连接ED并延长交AC于点F,已知∠DAC=58°.
如图,△ABC中,∠ABC=2∠C,AD为BC边上的高,延长AB到点E,使∠BDE=∠E,连接ED并延长交AC于点F,已知∠DAC=58°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
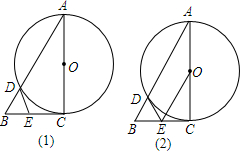
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
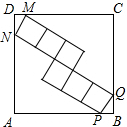 在边长为10的正方形ABCD中,内接有6个大小相同的正方形,P、Q、M、N是落在大正方形边上的小正方形的顶点,如图所示,则这六个小正方形的面积是( )
在边长为10的正方形ABCD中,内接有6个大小相同的正方形,P、Q、M、N是落在大正方形边上的小正方形的顶点,如图所示,则这六个小正方形的面积是( )| A. | $\frac{134}{25}$ | B. | $\frac{408}{25}$ | C. | $\frac{816}{25}$ | D. | $\frac{{12\sqrt{34}}}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
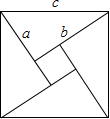 勾股定理是一条古老的数学定理,它神秘而美妙.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.它有很多种证明方法,其技巧各有不同.我国汉代数学家赵爽就根据弦图,利用面积法进行了证明.请你根据右图证明勾股定理.
勾股定理是一条古老的数学定理,它神秘而美妙.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.它有很多种证明方法,其技巧各有不同.我国汉代数学家赵爽就根据弦图,利用面积法进行了证明.请你根据右图证明勾股定理.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
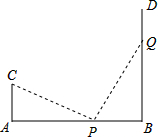 如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动4分钟后△CAP与△PQB全等.
如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动4分钟后△CAP与△PQB全等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com