
【题目】如图,A是半径为12cm的⊙O上的定点,动点P从A出发,以2πcm/s的速度沿圆周逆时针运动,当点P回到点A立即停止运动.
(1)如果∠POA=90°,求点P运动的时间;
(2)如果点B是OA延长线上的一点,AB=OA,那么当点P运动的时间为2s时,判断直线BP与⊙O的位置关系,并说明理由.

【答案】(1)点P运动的时间为3s或9s;(2)直线BP与⊙O相切,理由见解析.
【解析】
(1)当∠POA=90°时,点P运动的路程为⊙O周长的![]() 或
或![]() ,所以分两种情况进行分析即可得;
,所以分两种情况进行分析即可得;
(2)直线BP与⊙O的位置关系是相切,根据已知可证得OP⊥BP,即直线BP与⊙O相切.
(1)当∠POA=90°时,根据弧长公式可知点P运动的路程为⊙O周长的![]() 或
或![]() ,
,
设点P运动的时间为ts,
当点P运动的路程为⊙O周长的![]() 时,2πt=
时,2πt=![]() 2π12,解得t=3;
2π12,解得t=3;
当点P运动的路程为⊙O周长的![]() 时,2πt=
时,2πt=![]() 2π12,解得t=9,
2π12,解得t=9,
∴当∠POA=90°时,点P运动的时间为3s或9s;
(2)如图,当点P运动的时间为2s时,直线BP与⊙O相切.理由如下:
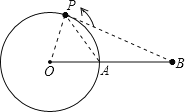
当点P运动的时间为2s时,点P运动的路程为4πcm,连接OP,PA,
∵半径AO=12,∴⊙O的周长为24π,
∴![]() 的长为⊙O周长的
的长为⊙O周长的![]() ,∴∠POA=60°,
,∴∠POA=60°,
∵OP=OA,∴△OAP是等边三角形,
∴OP=OA=AP,∠OAP=60°,
∵AB=OA,∴AP=AB,
∵∠OAP=∠APB+∠B,∴∠APB=∠B=30°,
∴∠OPB=∠OPA+∠APB=90°,
∴OP⊥BP,∴直线BP与⊙O相切.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,三角形ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).把三角形A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标,作出三角形ABC向右平移1个单位向下平移2个单位的图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,按以下步骤作图:
①以B为圆心,任意长为半径作弧,交AB于D,交BC于E;
②分别以D,E为圆心,以大于![]() DE的同样长为半径作弧,两弧交于点F;
DE的同样长为半径作弧,两弧交于点F;
③作射线BF交AC于G.
如果BG=CG,∠A=60°,那么∠ACB的度数为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCO中,AO=3,tan∠ACB=![]() ,以O为坐标原点,OC为
,以O为坐标原点,OC为![]() 轴,OA为
轴,OA为![]() 轴建立平面直角坐标系。设D,E分别是线段AC,OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动,设运动时间为
轴建立平面直角坐标系。设D,E分别是线段AC,OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动,设运动时间为![]() 秒。
秒。
(1)求直线AC的解析式;
(2)用含![]() 的代数式表示点D的坐标;
的代数式表示点D的坐标;
(3)当![]() 为何值时,△ODE为直角三角形?
为何值时,△ODE为直角三角形?
(4)在什么条件下,以Rt△ODE的三个顶点能确定一条对称轴平行于![]() 轴的抛物线?并请选择一种情况,求出所确定抛物线的解析式.
轴的抛物线?并请选择一种情况,求出所确定抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=![]() BC=1,则下列结论:
BC=1,则下列结论:
①∠CAD=30°②BD=![]() ③S平行四边形ABCD=ABAC④OE=
③S平行四边形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正确的个数是( )
,正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列应用题:
⑴某房间的面积为17.6m2,房间地面恰好由110块相同的正方形地砖铺成,每块地砖的边长是多少?
⑵已知第一个正方体水箱的棱长是60cm,第二个正方体水箱的体积比第一个水箱的体积的3倍还多81000 cm3,则第二个水箱需要铁皮多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
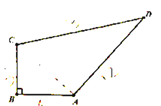
【题目】如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算这块土地的面积,以便估算产值,小明测得AB=4m,BC=3m,CD=13m.DA=12m.又已知∠B=90°,每平方米投入资金80元,预计销售后产值每平方米480元,试求出这块土地能产生多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填一填
(1)已知![]() ,则
,则![]() ________
________
(2)一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=_________.

(3)已知![]() ,则
,则![]() ___________________;
___________________;
(4)已知![]() ,
,![]() ,则
,则![]() _________________;
_________________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com