
如图,在平行四边形ABCD中,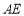 平分
平分 ,交
,交 于点
于点 ,
, 平分
平分 ,交
,交 于点
于点 ,
, 与
与 交于点
交于点 ,连接
,连接 ,
, .
.
(1)求证:四边形 是菱形;
是菱形;
(2)若 ,
,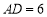 ,
, ,求
,求 的值.
的值.

(1)证明见解析
(2)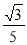
【解析】
试题分析:(1)根据AE平分∠BAD、BF平分∠ABC及平行四边形的性质可得AF=AB=BE,从而可知ABEF为平行四边形,又邻边相等,可知为菱形
(2)由菱形的性质可知AP的长及∠PAF=60°,过点P作PH⊥AD于H,即可得到PH、DH的长,从而可求tan∠ADP
试题解析:(1)∵AE平分∠BAD BF平分∠ABC
∴∠BAE=∠EAF ∠ABF=∠EBF
∵AD//BC
∴∠EAF=∠AEB ∠AFB=∠EBF
∴∠BAE=∠AEB ∠AFB=∠ABF
∴AB=BE AB=AF
∴AF=AB=BE
∵AD//BC
∴ABEF为平行四边形
又AB=BE
∴ABEF为菱形
(2)作PH⊥AD于H
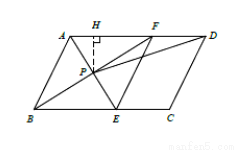
由∠ABC=60°而已(1)可知∠PAF=60°,PA=2,则有PH=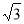 ,AH=1,∴DH=AD-AH=5
,AH=1,∴DH=AD-AH=5
∴tan∠ADP=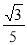
考点:1、平行四边形;2、菱形;3、直角三角形;4、三角函数


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:解答题
如图①,直角三角形AOB中,∠AOB=90°,AB平行于x轴,OA=2OB,AB=5,反比例函数 的图象经过点A.
(1)直接写出反比例函数的解析式;
(2)如图②,P(x,y)在(1)中的反比例函数图象上,其中1<x<8,连接OP,过O 作OQ⊥OP,且OP=2OQ,连接PQ.设Q坐标为(m,n),其中m<0,n>0,求n与m的函数解析式,并直接写出自变量m的取值范围;
(3)在(2)的条件下,若Q坐标为(m,1),求△POQ的面积.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:选择题
小军家距学校5千米,原来他骑自行车上学,学校为保障学生安全,新购进校车接送学生,若小车速度是他骑车速度的2倍,现在小军乘小车上学可以从家晚10分钟出发,结果与原来到校时间相同.设小军骑车的速度为x千米/小时,则所列方程正确的为( )
A. +
+ =
= B.
B. ﹣
﹣ =
= C.
C. +10=
+10= D.
D. ﹣10=
﹣10=
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(北京卷)数学(解析版) 题型:解答题
在正方形 外侧作直线
外侧作直线 ,点
,点 关于直线
关于直线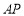 的对称点为
的对称点为 ,连接
,连接 ,其中
,其中 交直线
交直线 于点
于点 .
.
(1)依题意补全图1;
(2)若 ,求
,求 的度数;
的度数;
(3)如图2,若 ,用等式表示线段
,用等式表示线段 之间的数量关系,并证明.
之间的数量关系,并证明.


查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市通州区中考二模数学试卷(解析版) 题型:解答题
设 ,
, 是任意两个不等实数,我们规定:满足不等式
是任意两个不等实数,我们规定:满足不等式 ≤
≤ ≤
≤ 的实数
的实数 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为 . 对于一个函数,如果它的自变量
. 对于一个函数,如果它的自变量 与函数值
与函数值 满足:当m≤
满足:当m≤ ≤n时,有m≤
≤n时,有m≤ ≤n,我们就称此函数是闭区间
≤n,我们就称此函数是闭区间 上的“闭函数”.
上的“闭函数”.
(1)反比例函数 是闭区间
是闭区间 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数 是闭区间
是闭区间 上的“闭函数”,求此函数的表达式;
上的“闭函数”,求此函数的表达式;
(3)若二次函数 是闭区间
是闭区间 上的“闭函数”,直接写出实数
上的“闭函数”,直接写出实数 ,
, 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com