
在正方形 外侧作直线
外侧作直线 ,点
,点 关于直线
关于直线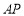 的对称点为
的对称点为 ,连接
,连接 ,其中
,其中 交直线
交直线 于点
于点 .
.
(1)依题意补全图1;
(2)若 ,求
,求 的度数;
的度数;
(3)如图2,若 ,用等式表示线段
,用等式表示线段 之间的数量关系,并证明.
之间的数量关系,并证明.


(1)见解析图形
∠ADF=25°
EF2+FD2=2AB2 证明见解析
【解析】
试题分析:(1)按照题意补全图形
应用轴对称的性质及正方形的性质、等腰三角形的性质解决问题
依照题意画出图形,然后应用轴对称的性质等进行解答
试题解析:(1)补全图形如图所示:
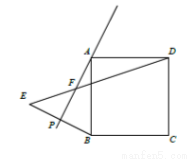
(2)
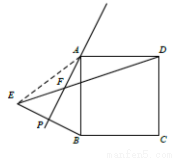
连接AE
则∠PAB=∠PAE=20°,AE=AB=AD
∵ABCD是正方形
∴∠BAD=90°
∴∠EAD=130°
∴∠ADF=25°
(3)
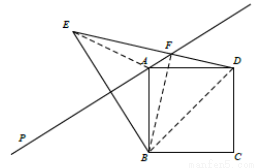
连接AE、BF、BD
由轴对称的性质可得:EF=BF,AE=AB=AD,∠ABF=∠AEF=∠ADF
∴∠BFD=∠BAD=90°
∴BF2+FD2=BD2
∴EF2+FD2=2AB2
考点:1、轴对称的性质;2、正方形的性质;3、勾股定理


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源:2014年初中毕业升学考试(四川南充卷)数学(解析版) 题型:填空题
如图,有一矩形纸片ABCD,AB=8,AD=17,将此矩形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB、AD(包括端点),设BA′=x,则x的取值范围是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:选择题
下列调查中,①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“神舟9号”的成功发射,对其零部件进行检查;④对乘坐某班次客车的乘客进行安检.其中适合采用抽样调查的是( )
A.① B.② C.③ D.④
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:填空题
如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:选择题
如图,四边形ABCD,AEFG都是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若AB=4,AE=1,则BH的长为( )

A.1 B.2 C.3 D.3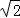
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(北京卷)数学(解析版) 题型:解答题
如图,在平行四边形ABCD中,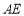 平分
平分 ,交
,交 于点
于点 ,
, 平分
平分 ,交
,交 于点
于点 ,
, 与
与 交于点
交于点 ,连接
,连接 ,
, .
.
(1)求证:四边形 是菱形;
是菱形;
(2)若 ,
,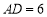 ,
, ,求
,求 的值.
的值.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(北京卷)数学(解析版) 题型:填空题
在平面直角坐标系 中,对于点
中,对于点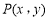 ,我们把点
,我们把点 叫做点
叫做点 的伴随点,已知点
的伴随点,已知点 的伴随点为
的伴随点为 ,点
,点 的伴随点为
的伴随点为 ,点
,点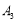 的伴随点为
的伴随点为 ,…,这样依次得到点
,…,这样依次得到点 ,
, ,
, ,…,
,…, ,….若点
,….若点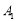 的坐标为(3,1),则点
的坐标为(3,1),则点 的坐标为 ,点
的坐标为 ,点 的坐标为 ;若点
的坐标为 ;若点 的坐标为(
的坐标为( ,
, ),对于任意的正整数
),对于任意的正整数 ,点
,点 均在
均在 轴上方,则
轴上方,则 ,
, 应满足的条件为 .
应满足的条件为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(内蒙古呼和浩特卷)数学(解析版) 题型:解答题
学校为了了解初三年级学生体育跳绳的训练情况,从初三年级各班随机抽取了50名学生进行了60秒跳绳的测试,并将这50名学生的测试成绩(即60秒跳绳的个数)从低到高分成六段记为第一到六组,最后整理成下面的频数分布直方图:请根据直方图中样本数据提供的信息解答下列问题.
(1)跳绳次数的中位数落在哪一组?由样本数据的中位数你能推断出学校初三年级学生关于60秒跳绳成绩的一个什么结论?
(2)若用各组数据的组中值(各小组的两个端点的数的平均数)代表各组的实际数据,求这50名学生的60秒跳绳的平均成绩(结果保留整数);
(3)若从成绩落在第一和第六组的学生中随机抽取2名学生,用列举法求抽取的2名学生恰好在同一组的概率.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(内蒙古包头、乌兰察布卷)数学(解析版) 题型:选择题
计算sin245°+cos30°•tan60°,其结果是( )
A.2 B.1 C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com