
如图①,直角三角形AOB中,∠AOB=90°,AB平行于x轴,OA=2OB,AB=5,反比例函数 的图象经过点A.
(1)直接写出反比例函数的解析式;
(2)如图②,P(x,y)在(1)中的反比例函数图象上,其中1<x<8,连接OP,过O 作OQ⊥OP,且OP=2OQ,连接PQ.设Q坐标为(m,n),其中m<0,n>0,求n与m的函数解析式,并直接写出自变量m的取值范围;
(3)在(2)的条件下,若Q坐标为(m,1),求△POQ的面积.

【解析】
试题分析:(1)如图①,在Rt△OAB中利用勾股定理计算出OB= ,OA=2
,OA=2 ,由于AB平行于x轴,则OC⊥AB,则可利用面积法计算出OC=2,在Rt△AOC中,根据勾股定理可计算出AC=4,得到A点坐标为(4,2),然后利用待定系数法确定反比例函数解析式为y=
,由于AB平行于x轴,则OC⊥AB,则可利用面积法计算出OC=2,在Rt△AOC中,根据勾股定理可计算出AC=4,得到A点坐标为(4,2),然后利用待定系数法确定反比例函数解析式为y=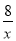 ;
;
(2)分别过P、Q做x轴垂线,垂足分别为D、H,如图②,先证明Rt△POH∽Rt△OQD,根据相似的性质得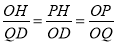 ,由于OP=2OQ,PH=y,OH=x,OD=﹣m,QD=n,则
,由于OP=2OQ,PH=y,OH=x,OD=﹣m,QD=n,则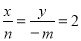 ,即有x=2n,y=﹣2m,而x、y满足y=
,即有x=2n,y=﹣2m,而x、y满足y=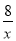 ,则2n•(﹣2m)=8,即mn=﹣2,当1<x<8时,1<y<8,所以1<﹣2m<8,解得﹣4<m<﹣
,则2n•(﹣2m)=8,即mn=﹣2,当1<x<8时,1<y<8,所以1<﹣2m<8,解得﹣4<m<﹣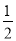 ;
;
(3)由于n=1时,m=﹣2,即Q点坐标为(﹣2,1),利用两点的距离公式计算出OQ= ,则OP=2OQ=2
,则OP=2OQ=2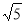 ,然后根据三角形面积公式求解.
,然后根据三角形面积公式求解.
试题解析:(1)如图①,
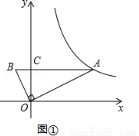
∵∠AOB=90°,
∴OA2+OB2=AB2,
∵OA=2OB,AB=5,
∴4OB2+OB2=25,解得OB=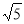 ,
,
∴OA=2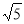 ,
,
∵AB平行于x轴,
∴OC⊥AB,
∴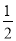 OC•AB=
OC•AB=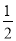 OB•OA,即OC=
OB•OA,即OC=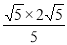 =2,
=2,
在Rt△AOC中,AC=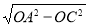 =4,
=4,
∴A点坐标为(4,2),
设过A点的反比例函数解析式为y=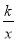 ,
,
∴k=4×2=8,
∴反比例函数解析式为y=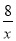 ;
;
(2)分别过P、Q作x轴垂线,垂足分别为D、H,如图②,
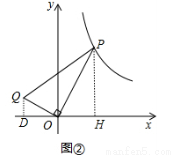
∵OQ⊥OP,
∴∠POH+∠QOD=90°,
∵∠POH+∠OPH=90°,
∴∠QOD=∠OPH,
∴Rt△POH∽Rt△OQD,
∴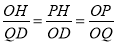 ,
,
∵P(x,y)在(1)中的反比例函数图象上,其中1<x<8,Q点点坐标为(m,n),其中m<0,n>0,OP=2OQ,
∴PH=y,OH=x,OD=﹣m,QD=n,
∴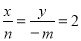 ,解得x=2n,y=﹣2m,
,解得x=2n,y=﹣2m,
∵y=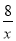 ,
,
∴2n•(﹣2m)=8,
∴mn=﹣2(﹣4<m<﹣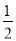 );
);
(3)∵n=1时,m=﹣2,即Q点坐标为(﹣2,1),
∴OQ=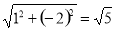 ,
,
∴OP=2OQ=2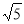 ,
,
∴S△POQ=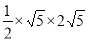 =5.
=5.
考点:1、待定系数法;2、坐标与图形的性质;3、相似三角形的判定与性质;4、勾股定理


科目:初中数学 来源:2014年初中毕业升学考试(四川宜宾卷)数学(解析版) 题型:填空题
如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:解答题
某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:选择题
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD为( )

A.2.5 B.1.6 C.1.5 D.1
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:选择题
下列调查中,①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“神舟9号”的成功发射,对其零部件进行检查;④对乘坐某班次客车的乘客进行安检.其中适合采用抽样调查的是( )
A.① B.② C.③ D.④
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:解答题
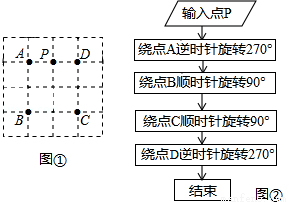
图①是电子屏幕的局部示意图,4×4网格的每个小正方形边长均为1,每个小正方形顶点叫做格点,点A,B,C,D在格点上,光点P从AD的中点出发,按图②的程序移动
(1)请在图①中用圆规画出光点P经过的路径;
(2)在图①中,所画图形是 轴对称 图形(填“轴对称”或“中心对称”),所画图形的周长是 (结果保留π).
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(吉林卷)数学(解析版) 题型:填空题
如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(北京卷)数学(解析版) 题型:解答题
如图,在平行四边形ABCD中,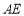 平分
平分 ,交
,交 于点
于点 ,
, 平分
平分 ,交
,交 于点
于点 ,
, 与
与 交于点
交于点 ,连接
,连接 ,
, .
.
(1)求证:四边形 是菱形;
是菱形;
(2)若 ,
,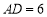 ,
, ,求
,求 的值.
的值.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(内蒙古呼和浩特卷)数学(解析版) 题型:选择题
已知线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为( )
A.(1,2) B.(2,9) C.(5,3) D.(–9,–4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com