
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.
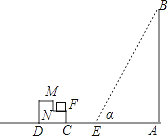
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
【答案】(1)15米;(2)小猫不能晒到太阳.
【解析】试题分析:(1)在Rt△ABE中,由tan56.3°=![]() ,即可求出AB=10tan56.3°,进而得出答案;
,即可求出AB=10tan56.3°,进而得出答案;
(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点P,与MC的交点为点Q,由∠BPA=45°,可得HQ=PH=0.3m,进而判断即可.
试题解析:(1)当α=56.3°时,在Rt△ABE中, ∵tan56.3°=![]() ≈1.50,
≈1.50,
∴AB=10tan56.3°≈10×1.50=15(m),
即楼房的高度约为15米;
(2)当α=45°时,小猫不能再晒到太阳,理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD交于点P,此时的影长AP=AB≈15m,
设MN的延长线交AD于点H,
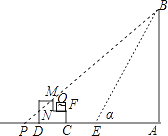
∵AC≈14.5m,NF=0.2m,
∴PH=AP﹣AC﹣CH≈15﹣14.5﹣0.2=0.3(m),
设直线MN与BP交于点Q,则HQ=PH=0.3m,
∴HQ=PH=0.3m,
∴点Q在MN上,
∴大楼的影子落在MN这个侧面上,
∴小猫不能晒到太阳.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
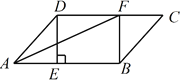
【题目】如图,在平行四边形![]() 中,过点
中,过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BE=5,AF平分∠DAB,求平行四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
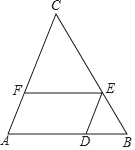
【题目】如图,已知△ABC中,D、E、F分别是边AB、BC、CA上的点,且EF∥AB,![]() =2.
=2.
(1)设![]() ,
,![]() .试用
.试用![]() 、
、![]() 表示
表示![]() ;
;
(2)如果△ABC的面积是9,求四边形ADEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ABC中,CA=CB,∠ACB=90°,点O是AB的中点.
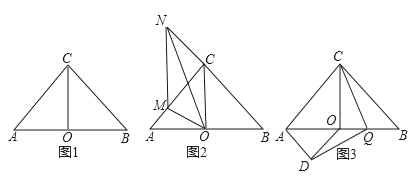
(1)如图1,求证:CO=BO;
(2)如图2,点M在边AC上,点N在边BC延长线上,MN﹣AM=CN,求∠MON的度数;
(3)如图3,AD∥BC,OD∥AC,AD与OD交于点D,Q是OB的中点,连接CQ、DQ,试判断线段CQ与DQ的关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,![]() ,
,![]() ,且∠ABC=900.
,且∠ABC=900.
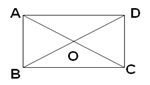
(1)求证:四边形ABCD是矩形.
(2)若∠ACB=300,AB=1,求①∠AOB的度数;②四边形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛。两个队各选出的5名选手的决赛成绩如图所示.
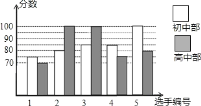
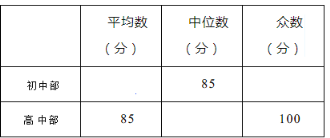
(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析表达式为,且
的解析表达式为,且![]() 与
与![]() 轴交于点D,直线
轴交于点D,直线![]() 经过点A,B,直线
经过点A,B,直线![]() ,
,![]() 交于点C.
交于点C.
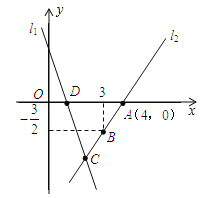
(1)求直线![]() 的解析式;
的解析式;
(2)求△ADC的面积;
(3)在直线![]() 上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图 1,等腰直角四边形 ABCD,AB=BC,∠ABC=90°.
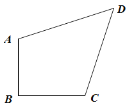
图 1
①若 AB=CD=1,AB∥CD,求对角线 BD 的长.
②若 AC⊥BD,求证:AD=CD;
(2) 如图 2,矩形 ABCD 的长宽为方程 ![]() -14x+40=0 的两根,其中(BC >AB),点 E 从 A 点出发,以 1 个单位每秒的速度向终点 D 运动;同时点 F 从 C 点出发,以 2 个单位每秒的速度向终点 B 运动,当点 E、F 运动过程中使四边形 ABFE 是等腰直角四边形时,求 EF 的长.
-14x+40=0 的两根,其中(BC >AB),点 E 从 A 点出发,以 1 个单位每秒的速度向终点 D 运动;同时点 F 从 C 点出发,以 2 个单位每秒的速度向终点 B 运动,当点 E、F 运动过程中使四边形 ABFE 是等腰直角四边形时,求 EF 的长.

图 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平移和翻折是初中阶段研究的两种重要的图形运动。
(平移运动)
(1)把笔尖放在数轴的原点,然后沿数轴向左移动 5 个单位长度,再向右移动3 个单位长度,这时笔尖的位置表示什么数?用算式可以将以上过程及结果表示为_____。
(2)把笔尖放在数轴的原点,第 1 次向左跳 2 个单位,紧接着第 2 次向右跳 4个单位,第 3 次向左跳 6 个单位,第 4 次向右跳 8 个单位,……依次规律跳,当它跳了 2019 次时,这时笔尖的位置表示的数是_____。

(翻折运动)
已知纸面上有一数轴,折叠纸面。

(3)若 1 表示的点与﹣1 表示的点重合,则﹣9 表示的点与_____表示的点重合。
(4)若 1 表示的点与﹣5 表示的点重合,回答以下问题:
① 3 表示的点与_____表示的点重合;
② 若数轴上 A,B 两点之间的距离为 2020(A 在 B 的左侧,且折痕与①折痕相同),且 A、B 两点经折叠后重合,则 A 点表示的数是 _____,B 点表示的数是_____;
(5)若数轴上折叠重合的两点表示的数分别为 a,b,那么数 c 表示的点与数_______表示的点也重合。(用含有 a,b,c 的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com