
【题目】已知![]() ,
, ![]() .
.
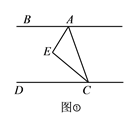
(1)如图①,当![]() 平分
平分![]() 时,求证:
时,求证: ![]() 平分
平分![]() ;
;
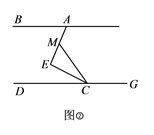
(2)如图②,移动直角顶点![]() ,使
,使![]() ,求证:
,求证: ![]() .
.
【答案】证明见解析.
【解析】试题分析:(1)由CE平分∠ACD可得出∠ACE=∠ECD,因为∠AEC=90°,所以∠EAC+∠ACE=90°,所以∠EAC+∠ECD=90°,又因为AB∥CD,所以∠BAC+∠ACD=180°,所以∠BAE+∠ECD=90°,所以∠EAC=∠BAE即AE平分∠BAC;(2)延长AE交DG于点F,
由∠MCE=∠ECF,∠MEC=∠FEC=90°结合三角形内角和可得出∠CME=∠CFE,进而得出∠MCG=2∠EFC,又因为AB∥CD,所以∠BAE=∠EFC,所以∠MCG=2∠BAE.
试题解析:
(1)∵CE平分∠ACD,
∴∠ACE=∠ECD,
∵∠AEC=90°,
∴∠EAC+∠ACE=90°,
∴∠EAC+∠ECD=90°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAE+∠ECD=90°,
∴∠EAC=∠BAE,
∴AE平分∠BAC;
(2)延长AE交DG于点F,
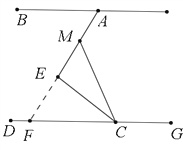
∵∠MCE=∠ECF,∠MEC=∠FEC=90°,
∴∠CME=∠CFE,
∴∠MCG=2∠EFC,
∵AB∥CD,
∴∠BAE=∠EFC,
∵∠MCG=2∠BAE.


科目:初中数学 来源: 题型:
【题目】甲、乙两人进行射击测试,每人10次射击成绩的平均数都是8.8环,方差分别是:S甲2=1,S乙2=0.8,则射击成绩较稳定的是 . (填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AC平分∠BAD,延长DC交AB的延长线于点E .
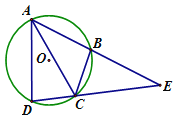
(1)若∠ADC=86°,求∠CBE的度数;
(2)若AC=EC,求证:AD=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P; 
(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1). 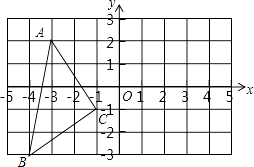
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点△A1 , B1 , C1的坐标(直接写答案):A1;B1;C1;
(3)△A1B1C1的面积为;
(4)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面运算正确的是( )
A. 3ab·3ac=6a2bc B. 4a2b·4b2a=16a2b2
C. 2x2·7x2=9x4 D. 3y2·2y2=6y4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com