
【题目】已知![]() ,
, ![]() .
.
(1)如图①,当![]() 平分
平分![]() 时,求证:
时,求证: ![]() 平分
平分![]() ;
;
(2)如图②,移动直角顶点![]() ,使
,使![]() ,求证:
,求证: ![]() .
.


【答案】证明见解析.
【解析】试题分析:(1)由CE平分∠ACD可得出∠ACE=∠ECD,因为∠AEC=90°,所以∠EAC+∠ACE=90°,所以∠EAC+∠ECD=90°,又因为AB∥CD,所以∠BAC+∠ACD=180°,所以∠BAE+∠ECD=90°,所以∠EAC=∠BAE即AE平分∠BAC;(2)延长AE交DG于点F,
由∠MCE=∠ECF,∠MEC=∠FEC=90°结合三角形内角和可得出∠CME=∠CFE,进而得出∠MCG=2∠EFC,又因为AB∥CD,所以∠BAE=∠EFC,所以∠MCG=2∠BAE.
试题解析:
(1)∵CE平分∠ACD,
∴∠ACE=∠ECD,
∵∠AEC=90°,
∴∠EAC+∠ACE=90°,
∴∠EAC+∠ECD=90°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠BAE+∠ECD=90°,
∴∠EAC=∠BAE,
∴AE平分∠BAC;
(2)延长AE交DG于点F,
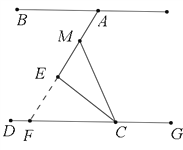
∵∠MCE=∠ECF,∠MEC=∠FEC=90°,
∴∠CME=∠CFE,
∴∠MCG=2∠EFC,
∵AB∥CD,
∴∠BAE=∠EFC,
∵∠MCG=2∠BAE.


科目:初中数学 来源: 题型:
【题目】如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( ) 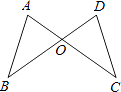
A.AB=DC
B.OB=OC
C.∠C=∠D
D.∠AOB=∠DOC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是秒. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面积是( ) 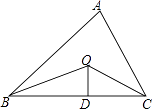
A.25
B.84
C.42
D.21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】婷婷在计算一个二项式的平方时,得到的正确结果是9x2+24xy+■,但最后一项不慎被污染了,这一项应是( )
A.16y2B.8y2C.4y2D.±16y2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com