【题目】函数y＝（x﹣2）2+1取得最小值时，x＝_____．
星级口算天天练系列答案
芒果教辅达标测试卷系列答案科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知y1关于x的二次函数y1=ax2+bx+c（a≠0）的图象过点（0，1），且在y轴的左侧，函数值y1随着自变量x的增大而增大．
（1）填空：a 0，b 0，c 0（用不等号连接）；
（2）已知一次函数y2=ax+b，当﹣1≤x≤1时，y2的最小值为﹣
且y1≤1，求y1关于x的函数解析式；
（3）设二次函数y1=ax2+bx+c的图象与x轴的一个交点为（﹣1，0），且当a≠﹣1时，一次函数y3=2cx+b﹣a与y4=
x﹣c（m≠0）的图象在第一象限内没有交点，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点O在线段AB上，点C、D分别是AO、BO的中点 
（1）AO=CO；BO=DO；
（2）若CO=3cm，DO=2cm，求线段AB的长度；
（3）若线段AB=10，小明很轻松地求得CD=5．他在反思过程中突发奇想：若点O在线段AB的延长线上，原有的结论“CD=5”是否仍然成立呢？请帮小明画出图形分析，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】1号探测气球从海拔5 m处出发，以l m/min的速度上升．与此同时，2号探测气球从海拔15 m处出发，以0.5 m/min的速度上升，两个气球都匀速上升了50 min.设气球上升的时间为x(min)(0≤x≤50)．
(1)根据题意，填写下表：
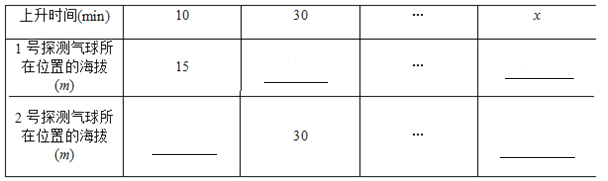
(2)在某时刻两个气球能否位于同一高度？如果能，这时气球上升了多长时间？位于什么高度？如果不能，请说明理由．
(3)当30≤x≤50时，两个气球所在位置的海拔最多相差多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
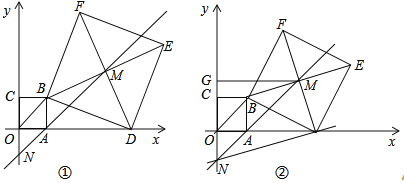
【题目】如图①，在直角坐标系中，点A的坐标为（1，0），以OA为一边在第一象限内作正方形OABC，点D是x轴正半轴上一动点（OD>1，且OD≠2），连接BD，以BD为边在第一象限内作正方形DBFE，设M为正方形DBFE的中心，直线MA交y轴于点N.如果定义：只有一组对角是直角的四边形叫做损矩形.
(1)、试找出图1中的一个损矩形 ；
(2)、试说明（1）中找出的损矩形一定有外接圆；
(3)、随着点D的位置变化，点N的位置是否会发生变化？若没有发生变化，求出点N的坐标；若发生变化，请说明理由.
(4)、在图②中，过点M作MG⊥y轴，垂足是点G，连结DN，若四边形DMGN为损矩形，求点D的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
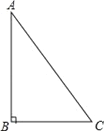
【题目】已知Rt△ABC中，∠B=90°，
（1）根据要求作图（尺规作图，保留作图痕迹，不写画法）：
①作∠BAC的平分线AD交BC于D；
②作线段AD的垂直平分线交AB于E，交AC于F，垂足为H；
③连接ED．
（2）在（1）的基础上写出一对全等三角形：△ ≌△ 并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，二次函数的图象与x轴交于A(-2，0)，B(4，0)两点，且函数的最大值为9.
(1)求二次函数的解析式；
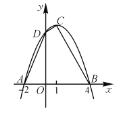
(2)设此二次函数图象的顶点为C，与y轴交点为D，求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
