
(本题满分8分)如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期期中考试数学试卷(解析版) 题型:填空题
抛掷一枚质地均匀的硬币2次,2次的结果都是正面朝上的概率是__________
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中数学试卷(解析版) 题型:解答题
在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图①,过点A在△ABC外作直线MN,BM⊥MN于M,CN⊥MN于N.①判断线段MN、BM、CN之间有何数量关系,并证明;
②若AM= ,BM=
,BM= ,AB=
,AB= ,试利用图①验证勾股定理
,试利用图①验证勾股定理 =
= ;
;
(2)如图②,过点A在△ABC内作直线MN,BM⊥MN于M,CN⊥MN于N,判断线段MN、BM、CN之间有何数量关系?(直接写出答案)

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中数学试卷(解析版) 题型:选择题
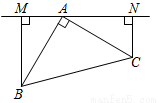
如图,在△ABC中, ,
, ,
, ,把
,把 沿
沿 边翻折成
边翻折成 ,(在同一个平面内)则
,(在同一个平面内)则 的长为
的长为

A.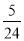 B.
B. C.
C. D.
D.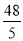
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中数学试卷(解析版) 题型:解答题
(本题满分10分)
【问题提出】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【初步思考】我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【深入探究】
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B.∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B.∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B.∠E都是锐角,若 ,则△ABC≌△DEF.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中数学试卷(解析版) 题型:填空题
如图,OP=1,过P作 且
且 ,得
,得 ;再过
;再过 作
作 且
且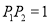 ,得
,得 ;又过
;又过 作
作 且
且 ,得
,得 ;……依此法继续作 下去,得
;……依此法继续作 下去,得 _______.
_______.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校初二上第一次检测二数学卷(解析版) 题型:解答题
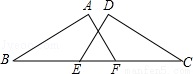
如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏徐州丰县中学八年级上学期第一次质检数学试卷(解析版) 题型:选择题
能判断两个三个角形全等的条件是( )
A.已知两角及一边相等
B.已知两边及一角对应相等
C.已知三条边对应相等
D.已知三个角对应相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com