
在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图①,过点A在△ABC外作直线MN,BM⊥MN于M,CN⊥MN于N.①判断线段MN、BM、CN之间有何数量关系,并证明;
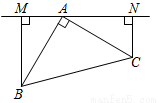
②若AM= ,BM=
,BM= ,AB=
,AB= ,试利用图①验证勾股定理
,试利用图①验证勾股定理 =
= ;
;
(2)如图②,过点A在△ABC内作直线MN,BM⊥MN于M,CN⊥MN于N,判断线段MN、BM、CN之间有何数量关系?(直接写出答案)

(1)证明见解析;(2)MN=BM-CN.
【解析】
试题分析:(1)①利用已知得出∠MAB=∠ACN,进而得出△MAB≌△NCA,进而得出BM=AN,AM=CN,即可得出线段MN、BM、CN之间的数量关系;
②利用S梯形MBCN=S△MAB+S△ABC+S△NCA=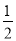 ab+
ab+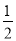 c2+
c2+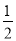 ab,S梯形MBCN=
ab,S梯形MBCN=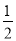 (BM+CN)×MN=
(BM+CN)×MN=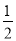 (a+b)2,进而得出答案;
(a+b)2,进而得出答案;
(2)利用已知得出∠MAB=∠ACN,进而得出△MAB≌△NCA,进而得出BM=AN,AM=CN,即可得出线段MN、BM、CN之间的数量关系.
试题解析:(1)①MN=BM+CN;
理由:∵∠MAB+∠NAC=90°,∠ACN+∠NAC=90°,
∴∠MAB=∠ACN,
在△MAB和△NCA中
 ,
,
∴△MAB≌△NCA(AAS),
∴BM=AN,AM=CN,
∴MN=AM+AN=BM+CN;
②由①知△MAB≌△NCA,
∴CN=AM=a,AN=BM=b,AC=BC=c,
∴MN=a+b,
∵S梯形MBCN=S△MAB+S△ABC+S△NCA=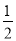 ab+
ab+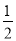 c2+
c2+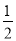 ab,S梯形MBCN=
ab,S梯形MBCN=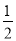 (BM+CN)×MN=
(BM+CN)×MN=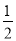 (a+b)2,
(a+b)2,
∴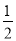 ab+
ab+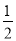 c2+
c2+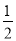 ab=
ab=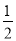 (a+b)2,
(a+b)2,
∴a2+b2=c2;
(2)MN=BM-CN;
理由:∵∠MAB+∠NAC=90°,∠ACN+∠NAC=90°,
∴∠MAB=∠ACN,
在△MAB和△NCA中
 ,
,
∴△MAB≌△NCA(AAS),
∴BM=AN,AM=CN,
∴MN=AN-AM=BM-CN.
考点:全等三角形的判定与性质.


科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期期中考试数学试卷(解析版) 题型:填空题
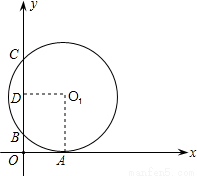
如图,一圆与平面直角坐标系中的x轴切于点A(8,0),与y轴交于点B(0,4),C(0,16),则该圆的直径为_________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期期中考试数学试卷(解析版) 题型:选择题
数据70、71、72、73、74的方差是( )
A. B.2 C.
B.2 C. D.
D.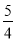
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市七年级上学期期中数学试卷(解析版) 题型:选择题
下列表示东台某天早晨、中午和午夜的温度(单位:℃),则下列说法正确的是 ( )

A.午夜与早晨的温差是11℃
B.中午与午夜的温差是0℃
C.中午与早晨的温差是11℃
D.中午与早晨的温差是3℃
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中数学试卷(解析版) 题型:解答题
正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点为顶点.
(1)在图①中,画一个面积为10的正方形;
(2)在图②、③中,分别画两个不全等的直角三角形,使它们的三边长都是无理数.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中数学试卷(解析版) 题型:填空题
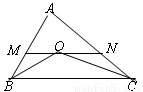
如图,BO平分∠ABC,CO平分∠ACB,过点O作MN∥BC,分别交AB、AC于点M、N,若AB=12,△AMN的周长为29,则AC= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省八年级上学期期中数学试卷(解析版) 题型:解答题
(本题满分8分)如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校初二上第一次检测二数学卷(解析版) 题型:选择题
如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( )

A.72° B.36° C.60° D.82°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com