
【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校。现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费。
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理。你认为哪种方案省时又省钱?为什么?
【答案】(1)、960套;(2)、甲、乙合作同时修理所需费用最少,理由见解析
【解析】
试题分析:(1)、首先设乙单独修需要x天,则甲单独修需要(x+20)天,根据总数列出方程进行求解;(2)、分别求出三种方案的费用,然后进行比较大小,选择用钱最少的.
试题解析:(1)、设乙单独修完需x天,则甲单独修完需(x+20)天。甲每天修16套,乙每天修24套。
根据题意,列方程为:16(x+20)=24x 解得: x=40(天) 经检验,符合题意
∴共有桌椅:16×(40+20)=960(套)
答:该中学库存桌椅960套。
(2)、由甲单独修理所需费用80×(40+20)+10×(40+20)=5400(元)
由乙单独修理所需费用:120×40+10×40=5200(元)
甲、 乙合作同时修理:完成所需天数:960×(![]() )=24(天)
)=24(天)
所需费用:(80+120+10)×24=5040(元)
∴由甲、乙合作同时修理所需费用最少
答:选择甲、乙合作修理。


科目:初中数学 来源: 题型:
【题目】已知,如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s,点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s,连接PQ,若设运动的时间为t(s)(0<t<2),解答下列问题:
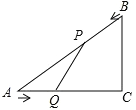
(1)设△AQP的面积为y(cm2),求y与t之间的函数关系式;
(2)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是( )
A. 13cm B. 6cm C. 5cm D. 4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个两位数,其十位数字为a,个位数字为b,将该两位数的两个数字颠倒,得到一个新的两位数,那么这个新两位数十位上的数字与个位上的数字的和与这个新两位数的积用代数式表示为__
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图1中线段BE、EF、FD之间的数量关系.
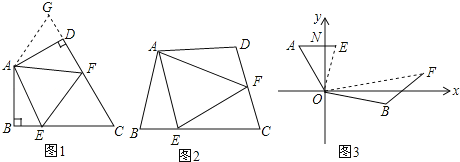
【初步探索】
小亮同学认为:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,则可得到 BE、EF、FD之间的数量关系是 .
【探索延伸】
在四边形ABCD中如图2,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,∠EAF=![]() ∠BAD,上述结论是否任然成立?说明理由.
∠BAD,上述结论是否任然成立?说明理由.
【结论运用】
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角(∠EOF)为70°,试求此时两舰艇之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com