
【题目】如图1,将两个完全相同的三角形纸片ABC和A′B′C重合放置,其中∠C=90°,∠B=∠B′=30°,AC=AC′=2.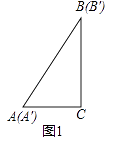
(1)如图2,固定△ABC,将△A′B′C绕点C旋转,当点A′恰好落在AB边上时,
①∠CA′B′=;旋转角ɑ=(0°<ɑ<90°),线段A′B′与AC的位置关系是;
(2)②设△A′BC的面积为S1 , △AB′C的面积为S2 , 则S1与S2的数量关系是什么?证明你的结论;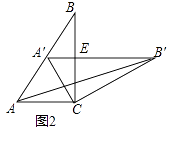
(3)如图3,∠MON=60°,OP平分∠MON,OP=PN=4,PQ∥MO交ON于点Q.若在射线OM上存在点F,使S△PNF=S△OPQ , 请直接写出相应的OF的长.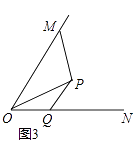
【答案】
(1)60°;60°;平行
(2)
解:S1=S2.理由如下:
∵A′B′∥AC,
∴A′E⊥BC,
在Rt△CA′E中,A′E= ![]() CA′=1,CE=
CA′=1,CE= ![]() A′E=
A′E= ![]() ,
,
∴S1= ![]() 12
12 ![]() =
= ![]() ,
,
S2= ![]() 2
2 ![]() =
= ![]() ,
,
∴S1=S2
(3)
如图3,作PF1∥ON交OM于F1,作PF2⊥OP交OM于F2,
∵∠MON=60°,OP平分∠MON,
∴∠POQ=∠POF1=30°,
∵PQ∥OM,PF1∥OQ,
∴四边形OQPF1为平行四边形,
∴PF1=OQ,
∴S△NF1P=S△POQ,
∵∠OPF2=90°,∠F2OP=30°,
∴∠OF2P=60°,
而∠F2F1P=∠MON=60°,
∴△F2F1P为等边三角形,
∴PF2=PF1,
由(1)中的结论得S△PNF2=S△OPQ,
∴点F1、点F2为满足条件的点,
在Rt△OPF2中,sin∠POF2= ![]() ,
,
∴OF2= ![]() =
= ![]() ,
,
∴PF2= ![]() OF2=
OF2= ![]() ,
,
∵PF1∥OQ,
∴∠OPF1=∠POQ=30°,
∴∠OPF1=∠POF1=30°,
∴OF1=PF1=PF2,
∴OF1= ![]() ,
,
综上所述,OF的长为 ![]() 或
或 ![]() .
.

【解析】解:(1)①如图1,∵∠C=90°,∠B=∠B′=30°,AC=AC′=2,
∴∠CAB=∠CA′B′=60°,BC=2 ![]() ,
,
如图2,
∵△A′B′C绕点C旋转,点A′恰好落在AB边上,
∴∠CAB=∠CA′B′=60°,CA=CA′,∠ACA′为旋转角,
∴△CAA′为等边三角形,
即旋转角为60°;
∵∠CA′B′=∠ACA′,
∴A′B′∥AC;
所以答案是60°;60°;平行;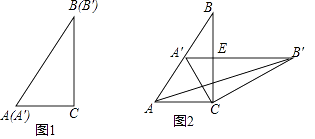
【考点精析】利用全等三角形的性质和图形的旋转对题目进行判断即可得到答案,需要熟知全等三角形的对应边相等; 全等三角形的对应角相等;每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
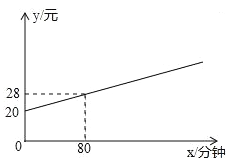
【题目】某通讯公司提供了两种移动电话收费方式:方式1,收月基本费20元,再以每分钟0.1元的价格按通话时间计费;方式2,收月基本费20元,送80分钟通话时间,超过80分钟的部分,以每分钟0.15元的价格计费.
下列结论:
①如图描述的是方式1的收费方法;
②若月通话时间少于240分钟,选择方式2省钱;
③若月通讯费为50元,则方式1比方式2的通话时间多;
④若方式1比方式2的通讯费多10元,则方式1比方式2的通话时间多100分钟.
其中正确的是( )
A.只有①② B.只有③④ C.只有①②③ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
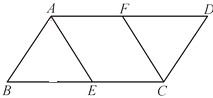
【题目】如图,在ABCD中,BC=2AB=4,点E,F分别是BC,AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,画一个长和宽分别为![]() 、
、![]() 的长方形,并将其按一定的方式进行旋转.
的长方形,并将其按一定的方式进行旋转.

![]() 你能得到几种不同的圆柱体?
你能得到几种不同的圆柱体?
![]() 把一个平面图形旋转成几何体,必须明确哪两个条件?
把一个平面图形旋转成几何体,必须明确哪两个条件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DEF中,已知AB=DE,∠A=∠D,若要得到△ABC≌△DEF,则还要补充一个条件,在下列补充方法:①AC=DF;②∠B=∠E;③∠B=∠F;④∠C=∠F ⑤BC=EF中,则错误结论的序号是__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家高斯在上学时曾经研究过这样一个问题,![]() ?
?
经过研究,这个问题的一般性结论是![]() ,其中
,其中![]() 为正整数,现在我们来研究一个类似的问题:
为正整数,现在我们来研究一个类似的问题:![]() ?
?
观察下面三个特殊的等式:
![]()
![]()
![]()
将这三个等式的两边相加,可以得到![]() .
.
读完这段材料,请你计算:
(1)![]() ________;(直接写出结果)
________;(直接写出结果)
(2)![]() ;(写出计算过程)
;(写出计算过程)
(3)![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
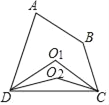
【题目】如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
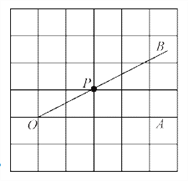
【题目】如图,在![]() 的正方形网格中,点P是
的正方形网格中,点P是![]() 的边OB上的一点.
的边OB上的一点.
(1)过点P画OB的垂线,交OA于点C;过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到直线__________的距离;
(3)线段__________的长度是点C到直线OB的距离;
(4)线段PC、PH、OC这三条线段大小关系是__________(用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)0﹣(﹣2)
(2)(+10)+(﹣14)
(3)5.6+(﹣0.9)+4.4+(﹣8.1)
(4)1﹣![]() +
+![]() ﹣
﹣![]() +
+![]()
(5)(﹣0.5)﹣(﹣3![]() )+2.75﹣(+7
)+2.75﹣(+7![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com