
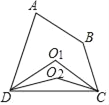
【题目】如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是_____.
【答案】175°
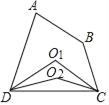
【解析】如图所示,∵∠ADC、∠BCD的平分线交于点O1,
∴∠O1DC+∠O1CD=![]() (∠ADC+∠DCB),
(∠ADC+∠DCB),
∵∠O1DC、∠O1CD的平分线交于点O2,
∴∠O2DC+∠O2CD=![]() (∠O1DC+∠O1CD)=
(∠O1DC+∠O1CD)=![]() (∠ADC+∠DCB),
(∠ADC+∠DCB),
同理可得,∠O3DC+∠O3CD=![]() (∠O2DC+∠O2CD)=
(∠O2DC+∠O2CD)=![]() (∠ADC+∠DCB),
(∠ADC+∠DCB),
由此可得,∠O5DC+∠O5CD=![]() (∠O4DC+∠O4CD)=
(∠O4DC+∠O4CD)=![]() (∠ADC+∠DCB),
(∠ADC+∠DCB),
∴△CO5D中,∠CO5D=180°﹣(∠O5DC+∠O5CD)=180°﹣![]() (∠ADC+∠DCB),
(∠ADC+∠DCB),
又∵四边形ABCD中,∠DAB+∠ABC=200°,
∴∠ADC+∠DCB=160°,
∴∠CO5D=180°﹣![]() ×160°=180°﹣5°=175°,
×160°=180°﹣5°=175°,
故答案为:175°.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12;第2次输出的结果是6;依次继续下去……第2018次输出的结果是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CM,交AB于点E,交AN于点F,现给出以下结论: ①AD=BD;②∠MAN=90°;③
,连接CM,交AB于点E,交AN于点F,现给出以下结论: ①AD=BD;②∠MAN=90°;③ ![]() =
= ![]() ;④∠ACM+∠ANM=∠MOB;⑤AE=
;④∠ACM+∠ANM=∠MOB;⑤AE= ![]() MF.
MF.
其中正确结论的个数是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和A′B′C重合放置,其中∠C=90°,∠B=∠B′=30°,AC=AC′=2.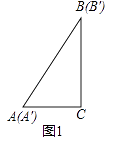
(1)如图2,固定△ABC,将△A′B′C绕点C旋转,当点A′恰好落在AB边上时,
①∠CA′B′=;旋转角ɑ=(0°<ɑ<90°),线段A′B′与AC的位置关系是;
(2)②设△A′BC的面积为S1 , △AB′C的面积为S2 , 则S1与S2的数量关系是什么?证明你的结论;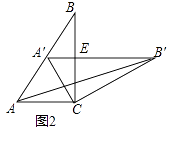
(3)如图3,∠MON=60°,OP平分∠MON,OP=PN=4,PQ∥MO交ON于点Q.若在射线OM上存在点F,使S△PNF=S△OPQ , 请直接写出相应的OF的长.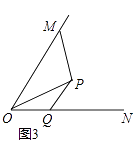
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数从1开始,按如图所表示的规律排列.规定图中第m行、第n列的位置
记作(m,n),如正整数8的位置是(2,3),则正整数139的位置记作_______.
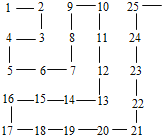
查看答案和解析>>
科目:初中数学 来源: 题型:
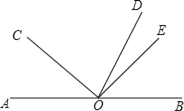
【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
(1)若∠AOC=48°,求∠DOE的度数.
(2)若∠AOC=α,则∠DOE= (用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某发电厂共有6台发电机发电,每台的发电量为300万千瓦/月.该厂计划从今年7月开始到年底,对6台发电机各进行一次改造升级.每月改造升级1台,这台发电机当月停机,并于次月再投入发电,每台发电机改造升级后,每月的发电量将比原来提高20%.已知每台发电机改造升级的费用为20万元.将今年7月份作为第1个月开始往后算,该厂第x(x是正整数)个月的发电量设为y(万千瓦).
(1)求该厂第2个月的发电量及今年下半年的总发电量;
(2)求y关于x的函数关系式;
(3)如果每发1千瓦电可以盈利0.04元,那么从第1个月开始,至少要到第几个月,这期间该厂的发电盈利扣除发电机改造升级费用后的盈利总额ω1(万元),将超过同样时间内发电机不作改造升级时的发电盈利总额ω2(万元)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的二次函数y═ax2+bx+c的图象,下列结论:①b2﹣4ac>0;②c>1;③2a﹣b<0;④a+b+c<0,其中正确的有( ) 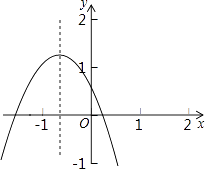
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com