
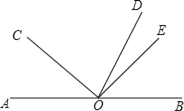
【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
(1)若∠AOC=48°,求∠DOE的度数.
(2)若∠AOC=α,则∠DOE= (用含α的代数式表示).
【答案】(1) ∠DOE=24°;(2)![]() α.
α.
【解析】
(1)先由邻补角定义求出∠BOC=180°-∠AOC=132°,再根据角平分线定义得到∠COD=![]() ∠BOC=66°,那么∠DOE=∠COE-∠COD=24°;
∠BOC=66°,那么∠DOE=∠COE-∠COD=24°;
(2)先由邻补角定义求出∠BOC=180°-∠AOC=180°-α,再根据角平分线定义得到∠COD=![]() ∠BOC,于是得到结论.
∠BOC,于是得到结论.
解:(1)∵O是直线AB上一点,
∴∠AOC+∠BOC=180°,
∵∠AOC=48°,
∴∠BOC=132°,
∵OD平分∠BOC,
∴∠COD=![]() ∠BOC=66°,
∠BOC=66°,
∵∠DOE=∠COE﹣∠COD,∠COE=90°,
∴∠DOE=90°﹣66°=24°;
(2)∵O是直线AB上一点,
∴∠AOC+∠BOC=180°,
∵∠AOC=α,
∴∠BOC=180°﹣α,
∵OD平分∠BOC,
∴∠COD=![]() ∠BOC=
∠BOC=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,
α,
∵∠DOE=∠COE﹣∠COD,∠COE=90°,
∴∠DOE=90°﹣(90°﹣![]() α)=
α)=![]() α.
α.
故答案为:![]() α.
α.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D. 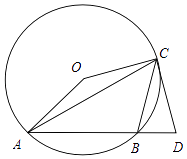
(1)求证:CD=CB;
(2)如果⊙O的半径为 ![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DEF中,已知AB=DE,∠A=∠D,若要得到△ABC≌△DEF,则还要补充一个条件,在下列补充方法:①AC=DF;②∠B=∠E;③∠B=∠F;④∠C=∠F ⑤BC=EF中,则错误结论的序号是__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
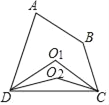
【题目】如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:观察下面由“※”组成的图案和算式,解答问题:
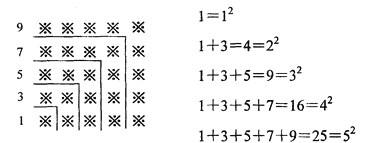
(1)请猜想1+3+5+7+9+…+19=_______________________;
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n+1) =___________;
(3)请用上述规律计算:51+53+55+…+2011+2013.
查看答案和解析>>
科目:初中数学 来源: 题型:
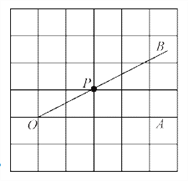
【题目】如图,在![]() 的正方形网格中,点P是
的正方形网格中,点P是![]() 的边OB上的一点.
的边OB上的一点.
(1)过点P画OB的垂线,交OA于点C;过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到直线__________的距离;
(3)线段__________的长度是点C到直线OB的距离;
(4)线段PC、PH、OC这三条线段大小关系是__________(用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的直径,CD是圆O的一条弦,且CD⊥AB于点E. 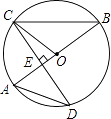
(1)若∠A=48°,求∠OCE的度数;
(2)若CD=4 ![]() ,AE=2,求圆O的半径.
,AE=2,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
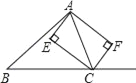
【题目】已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F.
(1)求证:四边形AECF是矩形;
(2)当△ABC满足什么条件时,四边形AECF是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国邮政部门规定:国内平信![]() 克以内(包括
克以内(包括![]() 克)每
克)每![]() 克需贴邮票
克需贴邮票![]() 元,不足
元,不足![]() 克重的以
克重的以![]() 克计算;超过
克计算;超过![]() 克的,超过部分每
克的,超过部分每![]() 克需加贴
克需加贴![]() 元,不足
元,不足![]() 克的以
克的以![]() 克计算.
克计算.
![]() 寄一封重
寄一封重![]() 克的国内平信,需贴邮票多少元?
克的国内平信,需贴邮票多少元?
![]() 某人寄一封国内平信贴了
某人寄一封国内平信贴了![]() 元邮票,此信重约多少克?
元邮票,此信重约多少克?
![]() 有
有![]() 人参加一次数学竞赛,每份答卷重
人参加一次数学竞赛,每份答卷重![]() 克,每个信封重
克,每个信封重![]() 克,将这
克,将这![]() 份答卷分装两个信封寄出,怎样装才能使所贴邮票金额最少?
份答卷分装两个信封寄出,怎样装才能使所贴邮票金额最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com