
【题目】如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CM,交AB于点E,交AN于点F,现给出以下结论: ①AD=BD;②∠MAN=90°;③
,连接CM,交AB于点E,交AN于点F,现给出以下结论: ①AD=BD;②∠MAN=90°;③ ![]() =
= ![]() ;④∠ACM+∠ANM=∠MOB;⑤AE=
;④∠ACM+∠ANM=∠MOB;⑤AE= ![]() MF.
MF.
其中正确结论的个数是( )
A.2
B.3
C.4
D.5
【答案】D
【解析】解:∵MN是⊙O的直径,AB⊥MN, ∴AD=BD, ![]() =
= ![]() ,∠MAN=90°(①②③正确)
,∠MAN=90°(①②③正确)
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴∠ACM+∠ANM=∠MOB(④正确)
∵∠MAE=∠AME,
∴AE=ME,∠EAF=∠AFM,
∴AE=EF,
∴AE= ![]() MF(⑤正确).
MF(⑤正确).
正确的结论共5个.
故选:D.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0 | 4 | 6 | 6 | 4 | 0 | … |
(1)求这个二次函数的表达式;
(2)直接写出当y<0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D. 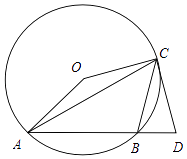
(1)求证:CD=CB;
(2)如果⊙O的半径为 ![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
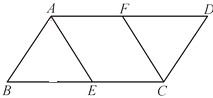
【题目】如图,在ABCD中,BC=2AB=4,点E,F分别是BC,AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,画一个长和宽分别为![]() 、
、![]() 的长方形,并将其按一定的方式进行旋转.
的长方形,并将其按一定的方式进行旋转.

![]() 你能得到几种不同的圆柱体?
你能得到几种不同的圆柱体?
![]() 把一个平面图形旋转成几何体,必须明确哪两个条件?
把一个平面图形旋转成几何体,必须明确哪两个条件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DEF中,已知AB=DE,∠A=∠D,若要得到△ABC≌△DEF,则还要补充一个条件,在下列补充方法:①AC=DF;②∠B=∠E;③∠B=∠F;④∠C=∠F ⑤BC=EF中,则错误结论的序号是__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
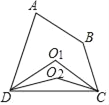
【题目】如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
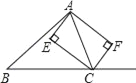
【题目】已知:如图,CE、CF分别是△ABC的内外角平分线,过点A作CE、CF的垂线,垂足分别为E、F.
(1)求证:四边形AECF是矩形;
(2)当△ABC满足什么条件时,四边形AECF是正方形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com