Question

【题目】抛物线y=ax2+bx+c（a≠0）上部分点的横坐标x，纵坐标y的对应值如表：

x	…	﹣2	﹣1	0	1	2	3	…
y	…	0	4	6	6	4	0	…

（1）求这个二次函数的表达式；
（2）直接写出当y＜0时x的取值范围．

Answer 1

【答案】
（1）解：设抛物线的表达式为：y=a（x+2）（x﹣3），

把（0，6）代入得：6=﹣6a，

a=﹣1，

∴抛物线的表达式为：y=﹣（x+2）（x﹣3）=﹣x2+x+6

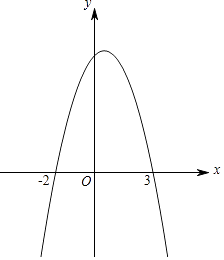
（2）解：如图所示，由图象得：当y＜0时，x的取值范围是：x＜﹣2或x＞3．

【解析】（1）根据待定系数法求二次函数的表达式；（2）画图象，根据图象直角写出当y＜0时x的取值范围．
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点，需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．才能正确解答此题．