
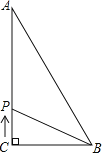
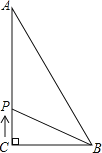
【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.
(1)当t为何值时,CP把△ABC的周长分成相等的两部分.
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时CP的长;(说明:直角三角形斜边上的中线等于斜边的一半)
(3)当t为何值时,△BCP为等腰三角形?
【答案】(1)6秒;(2)5cm;(3)当t=3秒或5.4秒或6秒或6.5秒时,△BCP为等腰三角形.
【解析】分析:(1)先由勾股定理求出△ABC的斜边AB=10cm,则△ABC的周长为24cm,所以当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,再根据时间=路程÷速度即可求解;
(2)根据中线的性质可知,点P在AB中点时,CP把△ABC的面积分成相等的两部分,进而求解即可;
(3)△BCP为等腰三角形时,分三种情况进行讨论:①CP=CB;②BC=BP;③PB=PC.
详解:(1)△ABC中,∵∠C=Rt∠,AC=8cm,BC=6cm,
∴AB=10cm,
∴△ABC的周长=8+6+10=24cm,
∴当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,
∴t=12÷2=6(秒);
(2)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时CA+AP=8+5=13(cm),∴t=13÷2=6.5(秒),
∴CP=![]() AB=
AB=![]() ×10=5cm;
×10=5cm;
(3)△BCP为等腰三角形时,分三种情况:
①如果CP=CB,那么点P在AC上,CP=6cm,此时t=6÷2=3(秒);
如果CP=CB,那么点P在AB上,CP=6cm,此时t=5.4(秒)
(点P还可以在AB上,此时,作AB边上的高CD,利用等面积法求得CD=4.8,再利用勾股定理求得DP=3.6,所以BP=7.2,AP=2.8,所以t=(8+2.8)÷2=5.4(秒))
②如果BC=BP,那么点P在AB上,BP=6cm,CA+AP=8+10-6=12(cm),此时t=12÷2=6(秒);
③如果PB=PC,那么点P在BC的垂直平分线与AB的交点处,即在AB的中点,此时CA+AP=8+5=13(cm),
t=13÷2=6.5(秒);
综上可知,当t=3秒或5.4秒或6秒或6.5秒时,△BCP为等腰三角形.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:
(1)∠DCF+![]() ∠D=90°;(2)∠AEF+∠ECF=90°;(3)S△BEC=2S△CEF;(4)若∠B=80°,则∠AEF=50°.
∠D=90°;(2)∠AEF+∠ECF=90°;(3)S△BEC=2S△CEF;(4)若∠B=80°,则∠AEF=50°.
其中一定成立的是_____(把所有正确结论的序号都填在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年春季,建阳区某服装商店分两次从批发市场购进同一款服装,数量之比是2:3,且第一、二次进货价分别为每件50元、40元,总共付了4400元的货款.
(1)求第一、二次购进服装的数量分别是多少件?
(2)由于该款服装刚推出时,很受欢迎,按每件70元销售了x件;后来,由于该服装滞销,为了及时处理库存,缓解资金压力,其剩余部分的按每件30元全部售完.当x的值至少为多少时,该服装商店才不会亏本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n),
则x2﹣4x+m=x2+(n+3)x+3n
∴![]()
解得:n=﹣7,m=﹣21.
∴另一个因式为(x﹣7),m的值为﹣21.
问题:
(1)若二次三项式x2﹣5x+6可分解为(x﹣2)(x+a),则a= ;
(2)若二次三项式2x2+bx﹣5可分解为(2x﹣1)(x+5),则b= ;
(3)仿照以上方法解答下面问题:若二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次模拟考试后,数学陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的百分比之和是14%;②第一组的百分比是2%;③自左到右第二、三、四组的频数比为3∶9∶8,然后布置学生(也请你一起)结合统计图完成下列问题:
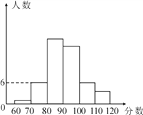
(1)全班学生是多少人?
(2)成绩不少于90分为优秀,那么全班成绩的优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
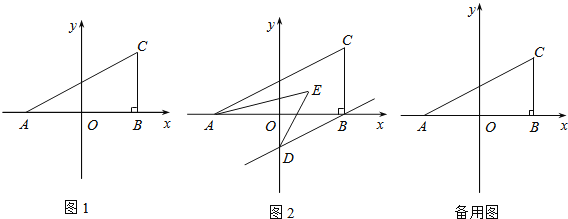
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足![]() ,过C作CB⊥x轴于B,
,过C作CB⊥x轴于B,
(1)求a,b的值;
(2)在y轴上是否存在点P,使得△ABC和△OCP的面积相等,求出P点坐标;
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,
①求:∠CAB+∠ODB的度数;
②求:∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王强参加了一场3000米的赛跑,他以6米/秒的速度跑了一段路程,又以4 米/秒的速度跑完了其余的路程,一共花了10分钟,王强以6米/ 秒的速度跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x+1)(x﹣m)交x轴于A,B两点(A在B的左侧,m>0),交y轴正半轴于点C,过点C作x轴的平行线交抛物线于另一点E,抛物线的对称轴交CE于点F,以C为圆心画圆,使⊙C经过点(0,2).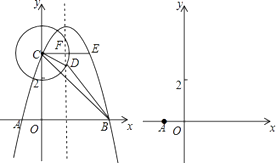
(1)直接写出OB,OC的长.(均用含m的代数式表示)
(2)当m>2时,判断点E与⊙C的位置关系,并说明理由.
(3)当抛物线的对称轴与⊙C相交时,其中下方的交点为D.连结CD,BD,BC.
①当m>3,且C,D,B三点在同一直线上时,求m的值.
②当△BCD是以CD为腰的等腰三角形时,求m的值.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为原点,A,B为数轴上两点,AB=15,且OA:OB=2
(1)A,B对应的数分别为 , .
(2)点A,B分别以2个单位/秒和5个单位/秒的速度相向而行,则几秒后A,B相距1个单位长度?
(3)点AB以(2)中的速度同时向右运动,点P从原点O以4个单位秒的速度向右运动,是否存在常数m,使得3AP+2PB﹣mOP为定值?若存在,请求出m值以及这个定值;若不存在,请说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com