
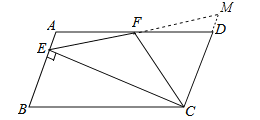
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:
(1)∠DCF+![]() ∠D=90°;(2)∠AEF+∠ECF=90°;(3)S△BEC=2S△CEF;(4)若∠B=80°,则∠AEF=50°.
∠D=90°;(2)∠AEF+∠ECF=90°;(3)S△BEC=2S△CEF;(4)若∠B=80°,则∠AEF=50°.
其中一定成立的是_____(把所有正确结论的序号都填在横线上)

【答案】(1)(2)(4)
【解析】分析:由平行四边形的性质和等腰三角形的性质得出(1)正确;
由ASA证明△AEF≌△DMF,得出EF=MF,∠AEF=∠M,由直角三角形斜边上的中线性质得出CF=![]() EM=EF,由等腰三角形的性质得出∠FEC=∠ECF,得出(2)正确;
EM=EF,由等腰三角形的性质得出∠FEC=∠ECF,得出(2)正确;
证出S△EFC=S△CFM,由MC>BE,得出S△BEC<2S△EFC,得出(3)错误;
由平行线的性质和互余两角的关系得出(4)正确;即可得出结论.
详解:(1)∵F是AD的中点,∴AF=FD.
∵在ABCD中,AD=2AB,∴AF=FD=CD,∴∠DFC=∠DCF.
∵AD∥BC,∴∠DFC=∠FCB,∠BCD+∠D=180°,∴∠DCF=∠BCF,∴∠DCF=![]() ∠BCD,∴∠DCF+
∠BCD,∴∠DCF+![]() ∠D=90°,故(1)正确;
∠D=90°,故(1)正确;
(2)延长EF,交CD延长线于M,如图所示:
∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A=∠MDF.
∵F为AD中点,∴AF=FD.在△AEF和△DFM中,∵∠A=∠FDM,AF=DF,∠AFE=∠DFM,∴△AEF≌△DMF(ASA),∴EF=MF,∠AEF=∠M.
∵CE⊥AB,∴∠AEC=90°,∴∠AEC=∠ECD=90°.
∵FM=EF,∴CF=![]() EM=EF,∴∠FEC=∠ECF,
EM=EF,∴∠FEC=∠ECF,
∴∠AEF+∠ECF=∠AEF+∠FEC=∠AEC=90°,故(2)正确;
(3)∵EF=FM,∴S△EFC=S△CFM.
∵MC>BE,∴S△BEC<2S△EFC,故(3)错误;
(4)∵∠B=80°,∴∠BCE=90°﹣80°=10°.
∵AB∥CD,∴∠BCD=180°﹣80°=100°,∴∠BCF=![]() ∠BCD=50°,∴∠FEC=∠ECF=50°﹣10°=40°,∴∠AEF=90°﹣40°=50°,故(4)正确.
∠BCD=50°,∴∠FEC=∠ECF=50°﹣10°=40°,∴∠AEF=90°﹣40°=50°,故(4)正确.
故答案为:(1)(2)(4).


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”,下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格(以下a、b、c为Rt△ABC的三边,且a<b<c):
表一 表二
a | b | c | a | b | c | |
3 | 4 | 5 | 6 | 8 | 10 | |
5 | 12 | 13 | 8 | 15 | 17 | |
7 | 24 | 25 | 10 | 24 | 26 | |
9 | 41 | 12 | 37 |
(1)仔细观察,表一中a为大于1的奇数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(2)仔细观察,表二中a为大于4的偶数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(3)我们还发现,表一中的三边长“3,4,5”与表二中的“6,8,10”成倍数关系,表一中的“5,12,13”与表二中的“10,24,26”恰好也成倍数关系……请直接利用这一规律计算:在Rt△ABC中,当![]() ,
,![]() 时,斜边c的值.
时,斜边c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解“数学思想作为对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和下表来表示(图、表都没制作完成). 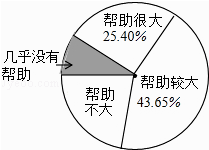
选项 | 帮助很大 | 帮助较大 | 帮助不大 | 几乎没有帮助 |
人数 | a | 543 | 269 | b |
根据图、表提供的信息.
(1)请问:这次共有多少名学生参与了问卷调查?
(2)算出表中a、b的值. (注:计算中涉及到的“人数”均精确到1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正方形ABCD中,点A,B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D→A匀速运动,同时动点Q以相同的速度在x轴正半轴上运动,当点P到达A点时,两点同时停止运动,设运动的时间为t秒.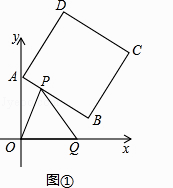
(1)当P点在边AB上运动时点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;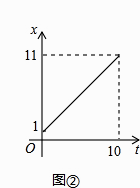
(2)求正方形边长及顶点C的坐标;
(3)在(1)中,设△OPQ的面积为S,求S与t的函数关系式并写出自变量的取值范围.
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等?若能,写出所有符合条件的t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是cm2 . 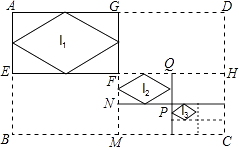
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是双曲线y= ![]() 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边做等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y= ![]() (k<0)上运动,则k的值是
(k<0)上运动,则k的值是 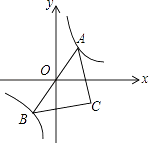
查看答案和解析>>
科目:初中数学 来源: 题型:
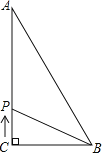
【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.
(1)当t为何值时,CP把△ABC的周长分成相等的两部分.
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时CP的长;(说明:直角三角形斜边上的中线等于斜边的一半)
(3)当t为何值时,△BCP为等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com