
 已知.在图中,AC⊥AB,EF⊥BC,AD⊥BC,∠1=∠2,试问AC⊥DG吗?请写出推理过程.
已知.在图中,AC⊥AB,EF⊥BC,AD⊥BC,∠1=∠2,试问AC⊥DG吗?请写出推理过程. 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
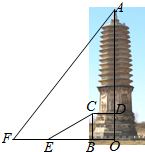 位于赤峰市宁城的“大明塔”是我国辽代的佛塔,距今已有1千多年的历史.如图,王强同学为测量大明塔的高度,在地面的点E处测得塔基BC上端C的仰角为30°,他又沿BE方向走了26米,到达点F处,测得塔顶端A的仰角为52°,已知塔基是以OB为半径的圆内接正八边形,B点在正八边形的一个顶点上,塔基半径OB=18米,塔基高BC=11米,求大明塔的高OA(结果保留到整数,
位于赤峰市宁城的“大明塔”是我国辽代的佛塔,距今已有1千多年的历史.如图,王强同学为测量大明塔的高度,在地面的点E处测得塔基BC上端C的仰角为30°,他又沿BE方向走了26米,到达点F处,测得塔顶端A的仰角为52°,已知塔基是以OB为半径的圆内接正八边形,B点在正八边形的一个顶点上,塔基半径OB=18米,塔基高BC=11米,求大明塔的高OA(结果保留到整数,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3x+5 |
| 2 |
| 2x-1 |
| 3 |
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在8×8的正方形网格中,有Rt△ABC,其顶点都在格点上.
如图,在8×8的正方形网格中,有Rt△ABC,其顶点都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com