
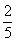 ,x2=
,x2=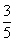
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
| ( ) |
| 3 |
| ( ) |
| 5 |
| ( ) |
| 7 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 | ||
3+
|
| 1 |
| x |
| 1 | ||||||||
3+
|
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 | ||
3+
|
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 | ||
3+
|
| 1 | ||||
3+
|
| 10 |
| 3 |
| 33 |
| 10 |
| 109 |
| 33 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 4 |
| ||
| 4 |
| 5 |
| 4 |
| ||
| 4 |
5+
| ||
| 4 |
5-
| ||
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| x2+3x-4=0 | ||||
| 2x2+x-1=0 | ||||
| 3x2-5x+2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011—2012学年安徽合肥古都中学七年级下期中考试数学试卷(带解析) 题型:解答题
先阅读下列知识,然后解答下面两个问题:
含有一个未知数,并且未知数的最高次指数是2的方程,叫做一元二次方程,如: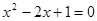 .
.
我们把它的一般形式记作: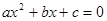 (a、b、c表示已知量,
(a、b、c表示已知量, 是未知数,a≠0),它的解的情况是:
是未知数,a≠0),它的解的情况是:
① 当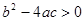 时,方程有两个不相等的解;
时,方程有两个不相等的解;
② 当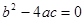 时,方程有两个相等的解(即一个解);
时,方程有两个相等的解(即一个解);
③ 当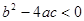 时,方程没有解;
时,方程没有解;
(1)一元二次方程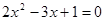 有几个解?为什么?
有几个解?为什么?
(2)当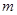 取何值时,关于
取何值时,关于 的一元二次方程
的一元二次方程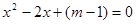 没有解?
没有解?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com