
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨∑÷Īū «Ņ…ĽÓ∂ĮĶńŃ‚–őļÕ∆Ĺ––ňńĪŖ–ő—ßĺŖ£¨“—÷™∆Ĺ––ňńĪŖ–őĹŌ∂ŐĶńĪŖ”ŽŃ‚–őĶńĪŖ≥§ŌŗĶ»£ģ

£®1£©‘ŕ“Ľīő ż—߼Ó∂Į÷–£¨ń≥–°◊ť—ß…ķĹęŃ‚–őĶń“ĽĪŖ”Ž∆Ĺ––ňńĪŖ–őĹŌ∂ŐĪŖ÷ōļŌ£¨įŕ∆ī≥…»ÁÕľ1ňý ĺĶńÕľ–ő£¨![]() ĺ≠ĻżĶ„
ĺ≠ĻżĶ„![]() £¨Ń¨Ĺ”
£¨Ń¨Ĺ”![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨ĻŘ≤ž∑ĘŌ÷£ļĶ„
£¨ĻŘ≤ž∑ĘŌ÷£ļĶ„![]() «
«![]() Ķń÷–Ķ„£ģ
Ķń÷–Ķ„£ģ
Ō¬√ś «ŃĹőĽ—ß…ķ”–īķĪŪ–‘Ķń÷§√ųňľ¬∑£ļ
ňľ¬∑£Ī£ļ≤Ľ–Ť◊ųł®÷ķŌŖ£¨÷ĪĹ”÷§»żĹ«–ő»ęĶ»£Ľ
ňľ¬∑2£ļ≤Ľ÷§»żĹ«–ő»ęĶ»£¨Ń¨Ĺ”![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £ģ°Ę
£ģ°Ę
°≠°≠
«Ž≤őŅľ…Ō√śĶńňľ¬∑£¨÷§√ųĶ„![]() «
«![]() Ķń÷–Ķ„£®÷Ľ–Ť”√“Ľ÷÷∑Ĺ∑®÷§√ų£©£Ľ
Ķń÷–Ķ„£®÷Ľ–Ť”√“Ľ÷÷∑Ĺ∑®÷§√ų£©£Ľ
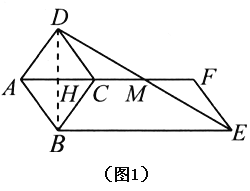
£®2£©»ÁÕľ2£¨‘ŕ£®1£©ĶńŐűľĢŌ¬£¨ĶĪ![]() Ī£¨—”≥§
Ī£¨—”≥§![]() °Ę
°Ę![]() ĹĽ”ŕĶ„
ĹĽ”ŕĶ„![]() £¨«ů
£¨«ů![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
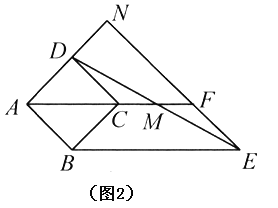
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨»Ű![]() £®
£®![]() ő™īů”ŕ
ő™īů”ŕ![]() Ķń≥£ ż£©£¨÷ĪĹ””√ļ¨
Ķń≥£ ż£©£¨÷ĪĹ””√ļ¨![]() Ķńīķ ż ĹĪŪ ĺ
Ķńīķ ż ĹĪŪ ĺ![]() Ķń÷Ķ£ģ
Ķń÷Ķ£ģ
°ĺīūįł°Ņ£®1£©ľŻĹ‚őŲ£Ľ£®2£©![]() £Ľ£®3£©
£Ľ£®3£©![]() .
.
°ĺĹ‚őŲ°Ņ
‘Ő‚∑÷őŲ£ļ£®1£©÷§∑®“Ľ£¨ņŻ”√Ń‚–ő–‘÷ Ķ√AB=CD£¨AB°őCD£¨ņŻ”√∆Ĺ––ňńĪŖ–őĶń–‘÷ Ķ√AB=EF£¨AB°őEF£¨‘ÚCD=EF£¨CD°őEF£¨‘Ŕłýĺ›∆Ĺ––ŌŖĶń–‘÷ Ķ√°ŌCDM=°ŌFEM£¨‘ÚŅ…łýĺ›°įAAS°ĪŇ–∂Ō°ųCDM°’°ųFEM£¨ňý“‘DM=EM£Ľ
÷§∑®∂Ģ£¨ņŻ”√Ń‚–ő–‘÷ Ķ√DH=BH£¨ņŻ”√∆Ĺ––ňńĪŖ–őĶń–‘÷ Ķ√AF°őBE£¨‘Ŕłýĺ›∆Ĺ––ŌŖ∑÷ŌŖ∂ő≥…Ī»ņż∂®ņŪĶ√ĶĹ![]() =1£¨ňý“‘DM=EM£Ľ
=1£¨ňý“‘DM=EM£Ľ
£®2£©”…°ųCDM°’°ųFEMĶ√ĶĹCM=FM£¨…ŤAD=a£¨CM=b£¨‘ÚFM=b£¨EF=AB=a£¨‘Ŕ÷§√ųňńĪŖ–őABCDő™’ż∑Ĺ–őĶ√ĶĹAC=![]() a£¨Ĺ”◊Ň÷§√ų°ųANFő™Ķ»—Ł÷ĪĹ«»żĹ«–őĶ√ĶĹNF=a+
a£¨Ĺ”◊Ň÷§√ų°ųANFő™Ķ»—Ł÷ĪĹ«»żĹ«–őĶ√ĶĹNF=a+![]() b£¨‘ÚNE=NF+EF=2a+
b£¨‘ÚNE=NF+EF=2a+![]() b£¨»Ľļůľ∆ň„
b£¨»Ľļůľ∆ň„![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®3£©”…”ŕ![]() £¨‘Ú
£¨‘Ú![]() £¨»ĽļůĪŪ ĺ≥Ų
£¨»ĽļůĪŪ ĺ≥Ų![]() £¨‘Ŕį—
£¨‘Ŕį—![]() īķ»Žľ∆ň„ľīŅ…£ģ
īķ»Žľ∆ň„ľīŅ…£ģ
‘Ő‚Ĺ‚őŲ£ļ£®1£©»ÁÕľ1£¨
÷§∑®“Ľ£ļ°ŖňńĪŖ–őABCDő™Ń‚–ő£¨°ŗAB=CD£¨AB°őCD£¨
°ŖňńĪŖ–őABEFő™∆Ĺ––ňńĪŖ–ő£¨°ŗAB=EF£¨AB°őEF£¨
°ŗCD=EF£¨CD°őEF£¨°ŗ°ŌCDM=°ŌFEM£¨‘ŕ°ųCDMļÕ°ųFEM÷–
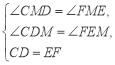 £¨°ŗ°ųCDM°’°ųFEM£¨°ŗDM=EM£¨ľīĶ„M «DEĶń÷–Ķ„£Ľ
£¨°ŗ°ųCDM°’°ųFEM£¨°ŗDM=EM£¨ľīĶ„M «DEĶń÷–Ķ„£Ľ
÷§∑®∂Ģ£ļ°ŖňńĪŖ–őABCDő™Ń‚–ő£¨°ŗDH=BH£¨
°ŖňńĪŖ–őABEFő™∆Ĺ––ňńĪŖ–ő£¨°ŗAF°őBE£¨
°ŖHM°őBE£¨°ŗ![]() =1£¨°ŗDM=EM£¨
=1£¨°ŗDM=EM£¨
ľīĶ„M «DEĶń÷–Ķ„£Ľ
£®2£©°Ŗ°ųCDM°’°ųFEM£¨°ŗCM=FM£¨
…ŤAD=a£¨CM=b£¨
°Ŗ°ŌABE=135°„£¨°ŗ°ŌBAF=45°„£¨
°ŖňńĪŖ–őABCDő™Ń‚–ő£¨°ŗ°ŌNAF=45°„£¨
°ŗňńĪŖ–őABCDő™’ż∑Ĺ–ő£¨°ŗAC=![]() AD=
AD=![]() a£¨
a£¨
°ŖAB°őEF£¨°ŗ°ŌAFN=°ŌBAF=45°„£¨
°ŗ°ųANFő™Ķ»—Ł÷ĪĹ«»żĹ«–ő£¨
°ŗNF=![]() AF=
AF=![]() £®
£®![]() a+b+b£©=a+
a+b+b£©=a+![]() b£¨
b£¨
°ŗNE=NF+EF=a+![]() b+a=2a+
b+a=2a+![]() b£¨°ŗ
b£¨°ŗ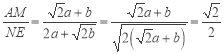 £Ľ
£Ľ
£®3£©°Ŗ![]() £¨°ŗ
£¨°ŗ![]() £¨
£¨
°ŗ![]()



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
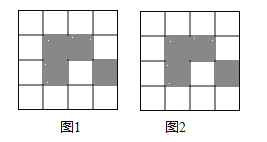
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ō¬Ń–4°Ń4ÕÝłŮÕľ∂ľ «”…16łŲŌŗÕ¨–°’ż∑Ĺ–ő◊ť≥…£¨√ŅłŲÕÝłŮÕľ÷–”–4łŲ–°’ż∑Ĺ–ő“—ÕŅ…Ō“ű”į£¨«Ž‘ŕŅ’į◊–°’ż∑Ĺ–ő÷–£¨įīŌ¬Ń–“™«ůÕŅ…Ō“ű”į£ģ
£®1£©‘ŕÕľ1÷–—°»°2łŲŅ’į◊–°’ż∑Ĺ–őÕŅ…Ō“ű”į£¨ Ļ6łŲ“ű”į–°’ż∑Ĺ–ő◊ť≥…“ĽłŲ÷––ń∂‘≥∆Õľ–ő£Ľ
£®2£©‘ŕÕľ2÷–—°»°2łŲŅ’į◊–°’ż∑Ĺ–őÕŅ…Ō“ű”į£¨ Ļ6łŲ“ű”į–°’ż∑Ĺ–ő◊ť≥…“ĽłŲ÷Š∂‘≥∆Õľ–ő£¨Ķę≤Ľ «÷––ń∂‘≥∆Õľ–ő£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»Ű“Ľ…»īįĽßīÚŅ™ļů£¨”√īįĻ≥Ĺę∆šĻŐ∂®£¨÷ų“™‘ň”√Ķńľłļő‘≠ņŪ « °£
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľňý ĺ£¨‘ŕ°ųABC÷–£¨°ŌA=60°„£¨BD°ĘCE∑÷Īū «AC°ĘAB…ŌĶńłŖ£¨H «BD°ĘCEĶńĹĽĶ„£¨‘Ú°ŌBHC=∂».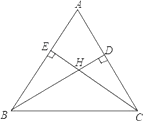
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»Űa£Ĺ2£¨a©Ā2b£Ĺ3£¨‘Ú2a2©Ā4abĶń÷Ķő™£®°°°°£©
A.2B.4C.6D.12
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨Ĺę◊ÝĪÍ‘≠Ķ„![]() —ō
—ō![]() ÷ŠŌÚ◊ů∆Ĺ“∆
÷ŠŌÚ◊ů∆Ĺ“∆![]() łŲĶ•őĽ≥§∂»Ķ√ĶĹĶ„
łŲĶ•őĽ≥§∂»Ķ√ĶĹĶ„![]() £¨ĻżĶ„
£¨ĻżĶ„![]() ◊ų
◊ų![]() ÷ŠĶń∆Ĺ––ŌŖĹĽ∑īĪ»ņżļĮ ż
÷ŠĶń∆Ĺ––ŌŖĹĽ∑īĪ»ņżļĮ ż![]() ĶńÕľŌů”ŕĶ„
ĶńÕľŌů”ŕĶ„![]() £¨
£¨![]() .
.
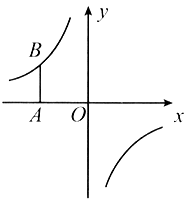
£®1£©«ů∑īĪ»ņżļĮ żĶńĹ‚őŲ Ĺ£Ľ
£®2£©»Ű![]() °Ę
°Ę![]() «ł√∑īĪ»ņżļĮ żÕľŌů…ŌĶńŃĹĶ„£¨«“
«ł√∑īĪ»ņżļĮ żÕľŌů…ŌĶńŃĹĶ„£¨«“![]() Ī£¨
Ī£¨![]() £¨÷ł≥ŲĶ„
£¨÷ł≥ŲĶ„![]() °Ę
°Ę![]() łųőĽ”ŕńńłŲŌůŌř£Ņ≤ĘľÚ“™ňĶ√ųņŪ”…£ģ
łųőĽ”ŕńńłŲŌůŌř£Ņ≤ĘľÚ“™ňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ¬ķ◊„x-5£ĺ3x+1ĶńxĶń◊Óīů’Ż ż «£® £©
A.0
B.-2
C.-3
D.-4
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ–°ĽŘłýĺ›—ßŌįļĮ żĶńĺ≠—ť£¨∂‘ļĮ ż![]() ĶńÕľŌů”Ž–‘÷ ĹÝ––Ńň—–ĺŅ£¨Ō¬√ś «–°ĽŘĶń—–ĺŅĻż≥Ő£¨«Ž≤Ļ≥šÕÍ≥…£ļ
ĶńÕľŌů”Ž–‘÷ ĹÝ––Ńň—–ĺŅ£¨Ō¬√ś «–°ĽŘĶń—–ĺŅĻż≥Ő£¨«Ž≤Ļ≥šÕÍ≥…£ļ

ĘŇļĮ ż![]() Ķń◊‘ĪšŃŅ
Ķń◊‘ĪšŃŅ![]() Ķń»°÷Ķ∑∂őß « £Ľ
Ķń»°÷Ķ∑∂őß « £Ľ
Ę∆Ń–ĪŪ£¨’“≥Ų![]() ”Ž
”Ž![]() Ķńľł◊ť∂‘”¶÷Ķ.
Ķńľł◊ť∂‘”¶÷Ķ.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆š÷–£¨![]() £Ľ
£Ľ
Ę«‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ![]() ÷–£¨√Ť≥Ų“‘…ŌĪŪ÷–łų∂”∂‘”¶÷Ķő™◊ÝĪÍĶńĶ„£¨≤ĘĽ≠≥Ųł√ļĮ żĶńÕľŌů£Ľ
÷–£¨√Ť≥Ų“‘…ŌĪŪ÷–łų∂”∂‘”¶÷Ķő™◊ÝĪÍĶńĶ„£¨≤ĘĽ≠≥Ųł√ļĮ żĶńÕľŌů£Ľ
Ę»–ī≥Ųł√ļĮ żĶń“ĽŐű–‘÷ £ļ .
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com