
【题目】如图所示,在△ABC中,∠A=60°,BD、CE分别是AC、AB上的高,H是BD、CE的交点,则∠BHC=度.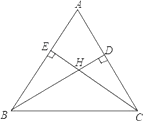
【答案】120
【解析】解:因为BD,CE分别是AC,AB 上的高,所以∠ADB=∠BEH=90°,
所以∠ABD=180°-∠ADB-∠A=180°-90°-60°=30°,
因此∠BHC=∠BEH+∠ABD=90°+30°=120°
【考点精析】通过灵活运用对顶角和邻补角和三角形的“三线”,掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个;1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内即可以解答此题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】某长途汽车站规定,乘客可以免费携带一定质量的行李,若超过该质量则需购买行李票,且行李票y(元)与行李质量x(千克)间的一次函数关系式为y=kx﹣5(k≠0),现知贝贝带了60千克的行李,交了行李费5元.
(1)若京京带了84千克的行李,则该交行李费多少元?
(2)旅客最多可免费携带多少千克的行李?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动手操作题:如何能把一个三角形分成两个等腰三角形吗?
实际上,一个三角形只要具备下列三个条件之一,都可以被分成两个等腰三角形:
①一个角为90°;②一个角是另一个的2倍(第三角必须大于45°);
③一个角是另一个角的3倍.今天,我们通过作图来验证这个结论。
(1)问题1:
如图,Rt△ABC中,求画一条直线l将△ABC分成两个等腰三角形.并说明直线l与△ABC
边上的交点D的位置.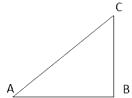
(2)问题2:
如图,△ABC中,∠ACB=80°, ∠BAC=40°,求画一条直线l把△ABC分成两个等腰三角形, 并在图中标注两个顶角的度数.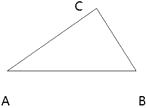
(3)问题3:
如图,△ABC中,∠ACB=120°, ∠BAC=40°,求画一条直线l把△ABC分成两个等腰三角形, 并在图中标注两个顶角的度数.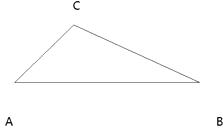
(4)问题:4:
如果等腰三角形能被一条直线分成两个等腰三角形,则原等腰三角形的顶角可以是°.(至少写出三个)
(5)拓展:已知△ABC的三条边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
A.6条
B.7条
C.8条
D.9条
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:
①平行四边形的对边相等;
②对角线相等的四边形是矩形;
③正方形既是轴对称图形,又是中心对称图形;
④一条对角线平分一组对角的平行四边形是菱形.
其中真命题的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(![]() 表示成绩,单位:分).
表示成绩,单位:分).![]() 组:
组:![]() ;
;![]() 组:
组:![]() ;
;![]() 组:
组:![]() ;
;![]() 组:
组:![]() ;
;![]() 组:
组:![]() ,并绘制如图两幅不完整的统计图.
,并绘制如图两幅不完整的统计图.
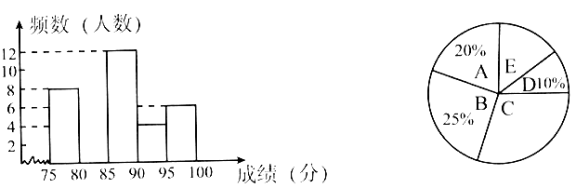
请根据图中信息,解答下列问题:
(1)参加初赛的选手共有 名,请补全频率分布直方图;
(2)扇形统计图中,![]() 组对应的圆心角是多少度?
组对应的圆心角是多少度?![]() 组人数占参赛选手的百分比是多少?
组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,![]() 组6名选手直接进入代表队,现要从
组6名选手直接进入代表队,现要从![]() 组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.

(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,![]() 经过点
经过点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,观察发现:点
,观察发现:点![]() 是
是![]() 的中点.
的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接![]() 交
交![]() 于点
于点![]() .、
.、
……
请参考上面的思路,证明点![]() 是
是![]() 的中点(只需用一种方法证明);
的中点(只需用一种方法证明);
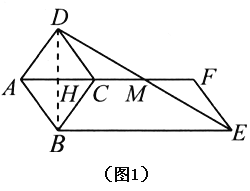
(2)如图2,在(1)的条件下,当![]() 时,延长
时,延长![]() 、
、![]() 交于点
交于点![]() ,求
,求![]() 的值;
的值;
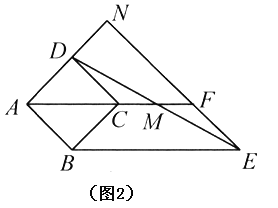
(3)在(2)的条件下,若![]() (
(![]() 为大于
为大于![]() 的常数),直接用含
的常数),直接用含![]() 的代数式表示
的代数式表示![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com