
分析 作辅助线,构建四边形和高线OG,先根据A(0,m-a),C (m+a,0),得EA=FC=a,易得Rt△PEA≌Rt△PFC(HL),则∠PCB=∠PAE,PC=PA,∠EPA=∠FPC,再证明:∠BPC=90°,所以∠AOC=∠BPC,又知:PB>PC,OA<OC,以P,B,C为顶点的三角形与△OAC相似中存在一种情况:
当△AOC∽△CPB中,∠OAC=∠PCB,证明OB=OC,根据中位线定理的推论得:PG=PC,由此得OP=OC,利用同角的三角函数得出结论.
解答 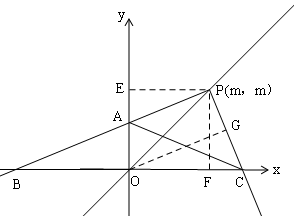 解:过P作PE⊥y轴于E,PF⊥x轴于F,
解:过P作PE⊥y轴于E,PF⊥x轴于F,
∵P(m,m),
∴OF=OE=PE=PF=m,
∵A(0,m-a),C (m+a,0),m>a>0,
∴EA=FC=a,
∴Rt△PEA≌Rt△PFC(HL),
∴∠PCB=∠PAE,PC=PA,∠EPA=∠FPC,
∴PB>PC,
∵∠EPF=90°,
∴∠EPA+∠APF=90°,
∴∠FPC+∠APF=90°,
∴∠BPC=90°,
∵∠AOC=90°,
∴∠AOC=∠BPC,
∵∠PAE=∠BAO,
当△AOC∽△CPB中,∠OAC=∠PCB,
∵∠PCB=∠BAO,
∴∠BAO=∠OAC,
∵AO=OA,∠AOB=∠AOC=90°,
∴△AOB≌△AOC,
∴OB=OC,
过O作OG⊥PC于G,
∴OG∥BP,
∴PG=CG,
∴OG是PC的中垂线,
∴OP=OC,
∴∠OPC=∠OCP,
∴tan∠OPC=tan∠OCP=$\frac{PF}{FC}=\frac{m}{a}$.
点评 本题考查了相似和全等三角形的性质和判定、解直角三角形、坐标与图形性质,根据点的坐标得出AE与CF相等是关键,对于P,B,C为顶点的三角形与△OAC相似时,注意三种情况中只成立一种情况.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:解答题
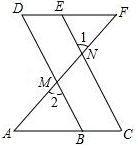 请将下列说理过程补充完整:
请将下列说理过程补充完整:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
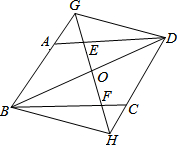 如图,在平行四边形ABCD中,AB=3,BC=4,∠ABC=60°,过对角线BD的中点O的直线GH分别交AD、BC于点E、F,交BA的延长线于点G,交DC的延长线于点H,连结GD、BH,则下列结论:①AG=CH,②DE+CF=5,③S四边形ABFE=3$\sqrt{3}$,④四边形BGDH为平行四边形.其中正确的有( )
如图,在平行四边形ABCD中,AB=3,BC=4,∠ABC=60°,过对角线BD的中点O的直线GH分别交AD、BC于点E、F,交BA的延长线于点G,交DC的延长线于点H,连结GD、BH,则下列结论:①AG=CH,②DE+CF=5,③S四边形ABFE=3$\sqrt{3}$,④四边形BGDH为平行四边形.其中正确的有( )| A. | ②③④ | B. | ①③④ | C. | ①②④ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com