
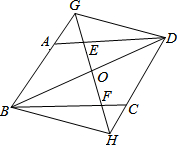
 如图,在平行四边形ABCD中,AB=3,BC=4,∠ABC=60°,过对角线BD的中点O的直线GH分别交AD、BC于点E、F,交BA的延长线于点G,交DC的延长线于点H,连结GD、BH,则下列结论:①AG=CH,②DE+CF=5,③S四边形ABFE=3$\sqrt{3}$,④四边形BGDH为平行四边形.其中正确的有( )
如图,在平行四边形ABCD中,AB=3,BC=4,∠ABC=60°,过对角线BD的中点O的直线GH分别交AD、BC于点E、F,交BA的延长线于点G,交DC的延长线于点H,连结GD、BH,则下列结论:①AG=CH,②DE+CF=5,③S四边形ABFE=3$\sqrt{3}$,④四边形BGDH为平行四边形.其中正确的有( )| A. | ②③④ | B. | ①③④ | C. | ①②④ | D. | ①②③ |
分析 利用平行四边形的性质得出AB∥CD即可得出∠OBG=∠ODH,进而得出△BOG≌△DOH即可判断出①正确;
进而判断出④正确,同①的方法判断出△AEG≌△CFH,进而得出AE=CF,即可求出DE+CF=4,即可得出②错误;利用平行四边形的面积公式求出平行四边形ABCD的面积,再判断出S四边形ABFE=S四边形CDEF即可.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BGO=∠DHO,∠OBG=∠ODH,
∵O是平行四边形ABCD的对角线的交点,
∴OB=OD,
在△BOG和△DOH中,$\left\{\begin{array}{l}{∠BGO=∠DHO}\\{∠OBG=∠ODH}\\{OB=OD}\end{array}\right.$,
∴△BOG≌△DOH,
∴BG=DH,
∴AG=CH,所以①正确;
∵BG=DH,BG∥DH,
∴四边形BGDH为平行四边形,所以④正确;
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠∠AEG=∠BFG,
∵∠BFG=∠CFH,
∴∠AEG=∠CFH,
在△AEG和△CFH中,$\left\{\begin{array}{l}{∠AEG=∠CFH}\\{∠AGE=∠CHF}\\{AG=CH}\end{array}\right.$,
∴△AEG≌△CFH,
∴AE=CF,
∴DE+CF=DE+AE=AD=BC=4,所以②错误;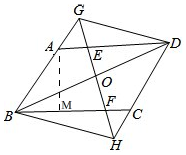 过点A作AM⊥BC于M,在Rt△ABM中,∠ABC=60°,AB=3,
过点A作AM⊥BC于M,在Rt△ABM中,∠ABC=60°,AB=3,
∴AM=ABsin∠ABC=3×sin60°=$\frac{3\sqrt{3}}{2}$,
∴S平行四边形ABCD=BC×AM=4×$\frac{3\sqrt{3}}{2}$=6$\sqrt{3}$,
∵△BOG≌△DOH,△AEG≌△CFH,
∴S四边形ABOE=S四边形CDOF,
易证:△BOF≌△DOE,
∴S△BOF=S△DOE,
∴S四边形ABFE=S四边形CDEF=$\frac{1}{2}$S平行四边形ABCD=$\frac{1}{2}$×6$\sqrt{3}$=3$\sqrt{3}$,所以③正确;
即:正确的有①③④,
故选B.
点评 此题是四边形综合题,主要考查了平行四边形的性质和判定,全等三角形的判定和性质,解本题的关键是判断出△BOG≌△DOH和△AEG≌△CFH.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
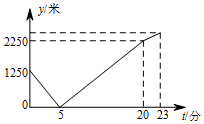 早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的图象如图所示,根据题意填空:
早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的图象如图所示,根据题意填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
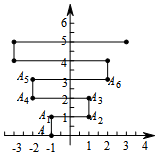 如图,在平面直角坐标系上有个点A(-1,0),点A第1次向上跳动一个单位至点A1(-1,1),紧接着第2次向右跳动2个单位至点A2(1,1),第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点A第2015次跳动至点A2015的坐标是( )
如图,在平面直角坐标系上有个点A(-1,0),点A第1次向上跳动一个单位至点A1(-1,1),紧接着第2次向右跳动2个单位至点A2(1,1),第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点A第2015次跳动至点A2015的坐标是( )| A. | (504,1008) | B. | (-504,1007) | C. | (503,1007) | D. | (-503,1008) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com