
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.

【答案】(1)证明见解析;(2)证明见解析;(3)EF2=2BE2+2DF2.
【解析】试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;
(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=![]() DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.
试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,
∴AF=AG,∠FAG=90°,
∵∠EAF=45°,
∴∠GAE=45°,
在△AGE与△AFE中,
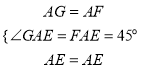 ,
,
∴△AGE≌△AFE(SAS);
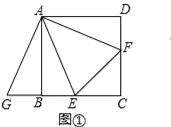
(2)设正方形ABCD的边长为a.
将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.
则△ADF≌△ABG,DF=BG.
由(1)知△AEG≌△AEF,
∴EG=EF.
∵∠CEF=45°,
∴△BME、△DNF、△CEF均为等腰直角三角形,
∴CE=CF,BE=BM,NF=![]() DF,
DF,
∴a﹣BE=a﹣DF,
∴BE=DF,
∴BE=BM=DF=BG,
∴∠BMG=45°,
∴∠GME=45°+45°=90°,
∴EG2=ME2+MG2,
∵EG=EF,MG=![]() BM=
BM=![]() DF=NF,
DF=NF,
∴EF2=ME2+NF2;
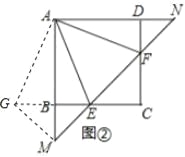
(3)EF2=2BE2+2DF2.
如图所示,延长EF交AB延长线于M点,交AD延长线于N点,
将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.
由(1)知△AEH≌△AEF,
则由勾股定理有(GH+BE)2+BG2=EH2,
即(GH+BE)2+(BM﹣GM)2=EH2
又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,
即2(DF2+BE2)=EF2


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.

(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线. 
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员统计了全班学生“1分钟跳绳”的次数,绘制成如下两幅统计图:

根据这两幅统计图的信息完成下列问题
(1)这个班共有学生多少人?并补全频数分布直方图;
(2)如果将“1分钟跳绳”的次数大于或等于180个定为优秀,请你求出这个班“1分钟跳绳”的次数达到优秀的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图□ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=600,AB=![]() BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=![]() BC 成立的个数有( )
BC 成立的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,某校规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对该校七年级部分学生参加户外活动的时间进行调查,并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:

(1)填空:这次调查的学生共 人,表示户外活动时间为1小时的扇形圆心角度数是 度;
(2)求参加户外活动的时间为1.5小时的学生人数,并补全频数分布直方图;
(3)若该校七年级有学生600人,请估计该校七年级学生参加户外活动的时间不少于1小时的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°.则∠AOD的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
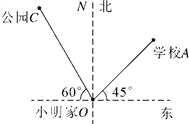
【题目】小明家O,学校A和公园C的平面示意图如图所示,图上距离OA=2cm,OC=2.5cm.
(1)学校A、公园C分别在小明家O的什么方向上?
(2)若学校A到小明家O的实际距离是400m,求公园C到小明家O的实际距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com