
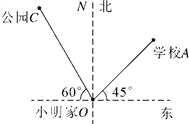
【题目】小明家O,学校A和公园C的平面示意图如图所示,图上距离OA=2cm,OC=2.5cm.
(1)学校A、公园C分别在小明家O的什么方向上?
(2)若学校A到小明家O的实际距离是400m,求公园C到小明家O的实际距离.
【答案】(1)学校A在小明家O的北偏东45°方向,公园C在小明家O的北偏西30°方向;(2)公园C到小明家O的实际距离是500m.
【解析】试题分析:(1)、根据方位的描述方法分别得出学校A和公园C的位置;(2)、首先根据学校A到小明家的图上距离和实际距离得出比例尺,然后根据比例尺和图上距离求出公园C到小明家的实际距离.
试题解析:解:(1)∵∠NOA=90°-45°=45°,∠CON=90°-60°=30°,
∴学校A在小明家O的北偏东45°方向,公园C在小明家O的北偏西30°方向.
(2)∵学校A到小明家O的实际距离是400m,且OA=2cm,
∴平面图上1cm代表的实际距离是200m,
∴平面图上2.5cm代表的实际距离是2.5×200=500(m),
故公园C到小明家O的实际距离是500m.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.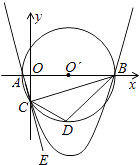
(1)求点C的坐标及抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条流水生产线上L1、L2、L3、L4、L5处各有一名工人在工作,现要在流水生产线上设置一个零件供应站P,使五人到供应站P的距离总和最小,这个供应站设置的位置是( )
![]()
A. L2处 B. L3处 C. L4处 D. 生产线上任何地方都一样
查看答案和解析>>
科目:初中数学 来源: 题型:
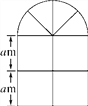
【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的收费;
(2)若有30名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,上七年级的小贝在一张纸上画了一条数轴,妹妹不知道它有什么用处,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题:
(1)被小猫遮住的是正数还是负数?
(2)被小狗遮住的整数有几个?
(3)此时小猫和小狗之间(即点A,B之间)的整数有几个?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com