
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.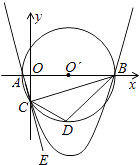
(1)求点C的坐标及抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由.
【答案】
(1)
解:∵以AB为直径作⊙O′,交y轴的负半轴于点C,
∴∠OCA+∠OCB=90°,
又∵∠OCB+∠OBC=90°,
∴∠OCA=∠OBC,
又∵∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴ ![]() .
.
又∵A(﹣1,0),B(9,0),
∴ ![]() ,
,
解得OC=3(负值舍去).
∴C(0,﹣3),
故设抛物线解析式为y=a(x+1)(x﹣9),
∴﹣3=a(0+1)(0﹣9),解得a= ![]() ,
,
∴二次函数的解析式为y= ![]() (x+1)(x﹣9),
(x+1)(x﹣9),
即y= ![]() x2﹣
x2﹣ ![]() x﹣3.
x﹣3.
(2)
解:∵AB为O′的直径,且A(﹣1,0),B(9,0),
∴OO′=4,O′(4,0),
∵点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,
∴∠BCD= ![]() ∠BCE=
∠BCE= ![]() ×90°=45°,
×90°=45°,
连接O′D交BC于点M,
则∠BO′D=2∠BCD=2×45°=90°,OO′=4,O′D= ![]() AB=5.
AB=5.
∴O′D⊥x轴
∴D(4,﹣5).
∴设直线BD的解析式为y=kx+b,
∴ ![]() ,
,
解得 ![]()
∴直线BD的解析式为y=x﹣9.
∵C(0,﹣3),
设直线BC的解析式为:y=ax+b,
∴ ![]() ,
,
解得: 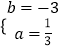 ,
,
∴直线BC的解析式为:y= ![]() x﹣3
x﹣3
(3)
解:假设在抛物线上存在点P,使得∠PDB=∠CBD,
解法一:设射线DP交⊙O′于点Q,则 ![]() .
.
分两种情况(如图所示):
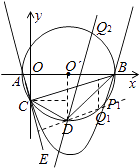
①∵O′(4,0),D(4,﹣5),B(9,0),C(0,﹣3).
∴把点C、D绕点O′逆时针旋转90°,使点D与点B重合,则点C与点Q1重合,
因此,点Q1(7,﹣4)符合 ![]() ,
,
∵D(4,﹣5),Q1(7,﹣4),
∴用待定系数法可求出直线DQ1解析式为y= ![]() x﹣
x﹣ ![]() .
.
解方程组 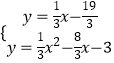
得 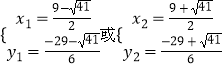
∴点P1坐标为( ![]() ,
, ![]() ),坐标为(
),坐标为( ![]() ,
, ![]() )不符合题意,舍去.
)不符合题意,舍去.
②∵Q1(7,﹣4),
∴点Q1关于x轴对称的点的坐标为Q2(7,4)也符合 ![]() .
.
∵D(4,﹣5),Q2(7,4).
∴用待定系数法可求出直线DQ2解析式为y=3x﹣17.
解方程组 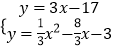
得 ![]() ,
,
即 ![]()
∴点P2坐标为(14,25),坐标为(3,﹣8)不符合题意,舍去.
∴符合条件的点P有两个:P1( ![]() ,
, ![]() ),P2(14,25).
),P2(14,25).
解法二:分两种情况(如图所示):
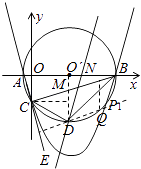
①当DP1∥CB时,能使∠PDB=∠CBD.
∵B(9,0),C(0,﹣3).
∴用待定系数法可求出直线BC解析式为y= ![]() x﹣3.
x﹣3.
又∵DP1∥CB,
∴设直线DP1的解析式为y= ![]() x+n.
x+n.
把D(4,﹣5)代入可求n=﹣ ![]() ,
,
∴直线DP1解析式为y= ![]() x﹣
x﹣ ![]() .
.
解方程组 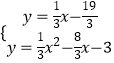
得 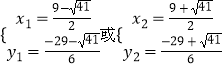
∴点P1坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )(不符合题意舍去).
)(不符合题意舍去).
②在线段O′B上取一点N,使BN=DM时,得△NBD≌△MDB(SAS),
∴∠NDB=∠CBD.
由①知,直线BC解析式为y= ![]() x﹣3.
x﹣3.
取x=4,得y=﹣ ![]() ,
,
∴M(4,﹣ ![]() ),
),
∴O′N=O′M= ![]() ,
,
∴N( ![]() ,0),
,0),
又∵D(4,﹣5),
∴直线DN解析式为y=3x﹣17.
解方程组 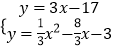
得 ![]() ,
,
![]()
∴点P2坐标为(14,25),坐标为(3,﹣8)不符合题意,舍去.
∴符合条件的点P有两个:P1( ![]() ,
, ![]() ),P2(14,25).
),P2(14,25).
解法三:分两种情况(如图所示):
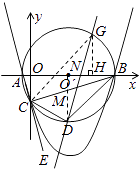
①求点P1坐标同解法二.
②过C点作BD的平行线,交圆O′于G,
此时,∠GDB=∠GCB=∠CBD.
由(2)题知直线BD的解析式为y=x﹣9,
又∵C(0,﹣3)
∴可求得CG的解析式为y=x﹣3,
设G(m,m﹣3),作GH⊥x轴交于x轴与H,
连接O′G,在Rt△O′GH中,利用勾股定理可得,m=7,
由D(4,﹣5)与G(7,4)可得,
DG的解析式为y=3x﹣17,
解方程组 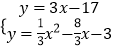
得 ![]() ,
,
即 ![]()
∴点P2坐标为(14,25),坐标为(3,﹣8)不符合题意舍去.
∴符合条件的点P有两个:P1( ![]() ,
, ![]() ),P2(14,25).
),P2(14,25).
【解析】(1)已知了A、B两点的坐标即可得出OA、OB的长,在直角三角形ACB中由于OC⊥AB,因此可用射影定理求出OC的长,即可得出C点的坐标.然后用待定系数法即可求出抛物线的解析式;(2)本题的关键是得出D点的坐标,CD平分∠BCE,如果连接O′D,那么根据圆周角定理即可得出∠DO′B=2∠BCD=∠BCE=90°由此可得出D的坐标为(4,﹣5).根据B、D两点的坐标即可用待定系数法求出直线BD的解析式;(3)本题要分两种情况进行讨论:
①过D作DP∥BC,交D点右侧的抛物线于P,此时∠PDB=∠CBD,可先用待定系数法求出直线BC的解析式,然后根据BC与DP平行,那么直线DP的斜率与直线BC的斜率相同,因此可根据D的坐标求出DP的解析式,然后联立直线DP的解析式和抛物线的解析式即可求出交点坐标,然后将不合题意的舍去即可得出符合条件的P点.②同①的思路类似,先作与∠CBD相等的角:在O′B上取一点N,使BN=BM.可通过证△NBD≌△MDB,得出∠NDB=∠CBD,然后同①的方法一样,先求直线DN的解析式,进而可求出其与抛物线的交点即P点的坐标.综上所述可求出符合条件的P点的值.


科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线. 
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,某校规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对该校七年级部分学生参加户外活动的时间进行调查,并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:

(1)填空:这次调查的学生共 人,表示户外活动时间为1小时的扇形圆心角度数是 度;
(2)求参加户外活动的时间为1.5小时的学生人数,并补全频数分布直方图;
(3)若该校七年级有学生600人,请估计该校七年级学生参加户外活动的时间不少于1小时的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°.则∠AOD的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD. 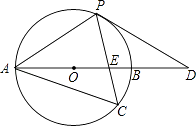
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若 ![]() :
: ![]() =1:2,求AE:EB:BD的值(请你直接写出结果);
=1:2,求AE:EB:BD的值(请你直接写出结果);
(3)若点C是弧AB的中点,已知AB=4,求CECP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b与双曲线y=![]() 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
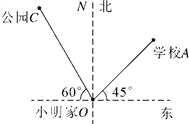
【题目】小明家O,学校A和公园C的平面示意图如图所示,图上距离OA=2cm,OC=2.5cm.
(1)学校A、公园C分别在小明家O的什么方向上?
(2)若学校A到小明家O的实际距离是400m,求公园C到小明家O的实际距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com