【题目】把长方形ABCD沿AE折叠后，D点恰与BC边上的F重合，如图，已知AB=8，BC=10，求EC的长．
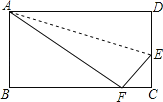
【答案】EC的长度为3．
【解析】
试题分析：由长方形ABCD沿AE折叠后，D点恰与BC边上的F重合，可得AF=AD=10，DE=EF，然后设EC=x，则DE=EF=CD﹣EC=8﹣x，首先在Rt△ABF中，利用勾股定理求得BF的长，继而可求得CF的长，然后在Rt△CEF中，由勾股定理即可求得方程：x2+42=（8﹣x）2，解此方程即可求得答案．
解：∵四边形ABCD是长方形，
∴∠B=∠C=90°，AD=BC=10，CD=AB=8，
∵△ADE折叠后得到△AFE，
∴AF=AD=10，DE=EF，
设EC=x，则DE=EF=CD﹣EC=8﹣x，
∵在Rt△ABF中，AB2+BF2=AF2，
∴82+BF2=102，
∴BF=6，
∴CF=BC﹣BF=10﹣6=4，
∵在Rt△EFC中，EC2+CF2=EF2，
∴x2+42=（8﹣x）2，
解得：x=3，
即EC的长度为3．
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，有一Rt△ABC，且A（﹣1，3），B（﹣3，﹣1），C（﹣3，3），已知△A1AC1是由△ABC旋转得到的．
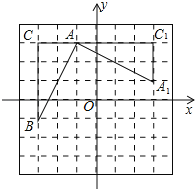
（1）请写出旋转中心的坐标是 ，旋转角是 度；
（2）以（1）中的旋转中心为中心，画出△A1AC1顺时针旋转90°的三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】根据下列已知条件，能唯一画出△ABC的是（ ）
A. AB＝3，BC＝4，CA＝8 B. ∠A＝60°，∠B＝45°，AB＝4
C. AB＝4，BC＝3，∠A＝30° D. ∠C＝90°，AB＝6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，把长为40cm，宽30cm的长方形硬纸板，剪掉2个小正方形和2个小长方形（阴影部分即剪掉的部分），将剩余的部分拆成一个有盖的长方体盒子，设剪掉的小正方形边长为xcm（纸板的厚度忽略不计）
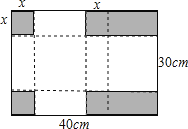
（1）长方体盒子的长、宽、高分别为多少？（单位：cm）
（2）若折成的一个长方体盒于表面积是950cm2，求此时长方体盒子的体积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题背景：在△ABC中，AB、BC、AC三边的长分别为
、
、
，求这个三角形的面积小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．
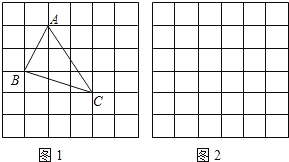
（1）请你将△ABC的面积直接填写在横线上．
（2）画△DEF，DE、EF、DF三边的长分别为
、
、
①判断三角形的形状，说明理由．
②求这个三角形的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com