
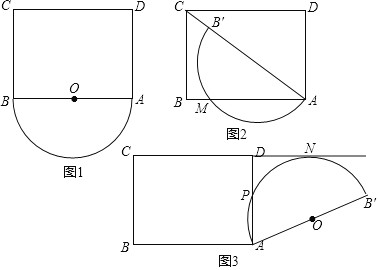
ЁОЬтФПЁПвбжЊОиаЮABCDЃЌAB=4ЃЌBC=3ЃЌвдABЮЊжБОЖЕФАыдВOдкОиаЮABCDЕФЭтВПЃЈШчЭМЃЉЃЌНЋАыдВOШЦЕуAЫГЪБеыа§зЊІСЖШЃЈ0ЁуЁмІСЁм180ЁуЃЉ
ЃЈ1ЃЉАыдВЕФжБОЖТфдкЖдНЧЯпACЩЯЪБЃЌШчЭМЫљЪОЃЌАыдВгыABЕФНЛЕуЮЊMЃЌЧѓAMЕФГЄЃЛ
ЃЈ2ЃЉАыдВгыжБЯпCDЯрЧаЪБЃЌЧаЕуЮЊNЃЌгыЯпЖЮADЕФНЛЕуЮЊPЃЌШчЭМЫљЪОЃЌЧѓСгЛЁAPЕФГЄЃЛ
ЃЈ3ЃЉдка§зЊЙ§ГЬжаЃЌАыдВЛЁгыжБЯпCDжЛгавЛИіНЛЕуЪБЃЌЩшДЫНЛЕугыЕуCЕФОрРыЮЊdЃЌжБНгаДГіdЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉAM=![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() =
=![]() ІаЃЛЃЈ3ЃЉ4-
ІаЃЛЃЈ3ЃЉ4-![]() ЁмdЃМ4Лђd=4+
ЁмdЃМ4Лђd=4+![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉСЌНгBЁфMЃЌдђЁЯBЁфMA=90ЁуЃЌдкRtЁїABCжаЃЌРћгУЙДЙЩЖЈРэПЩЧѓГіACЕФГЄЖШЃЌгЩЁЯB=ЁЯBЁфMA=90ЁуЁЂЁЯBCA=ЁЯMABЁфПЩЕУГіЁїABCЁзЁїAMBЁфЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪПЩЧѓГіAMЕФГЄЖШЃЛ
ЃЈ2ЃЉСЌНгOPЁЂONЃЌЙ§ЕуOзїOGЁЭADгкЕуGЃЌдђЫФБпаЮDGONЮЊОиаЮЃЌНјЖјПЩЕУГіDGЁЂAGЕФГЄЖШЃЌдкRtЁїAGOжаЃЌгЩAO=2ЁЂAG=1ПЩЕУГіЁЯOAG=60ЁуЃЌНјЖјПЩЕУГіЁїAOPЮЊЕШБпШ§НЧаЮЃЌдйРћгУЛЁГЄЙЋЪНМДПЩЧѓГіСгЛЁAPЕФГЄЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩжЊЃКЁїAOPЮЊЕШБпШ§НЧаЮЃЌИљОнЕШБпШ§НЧаЮЕФаджЪПЩЧѓГіOGЁЂDNЕФГЄЖШЃЌНјЖјПЩЕУГіCNЕФГЄЖШЃЌЛГіЕуBЁфдкжБЯпCDЩЯЕФЭМаЮЃЌдкRtЁїABЁфDжаЃЈЕуBЁфдкЕуDзѓБпЃЉЃЌРћгУЙДЙЩЖЈРэПЩЧѓГіBЁфDЕФГЄЖШНјЖјПЩЕУГіCBЁфЕФГЄЖШЃЌдйНсКЯЭМаЮМДПЩЕУГіЃКАыдВЛЁгыжБЯпCDжЛгавЛИіНЛЕуЪБdЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉдкЭМ2жаЃЌСЌНгBЁфMЃЌдђЁЯBЁфMA=90ЁуЃЎ
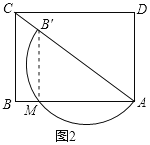
дкRtЁїABCжаЃЌAB=4ЃЌBC=3ЃЌ
ЁрAC=5ЃЎ
ЁпЁЯB=ЁЯBЁфMA=90ЁуЃЌЁЯBCA=ЁЯMABЁфЃЌ
ЁрЁїABCЁзЁїAMBЁфЃЌ
Ёр![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЌ
ЃЌ
ЁрAM=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЭМ3жаЃЌСЌНгOPЁЂONЃЌЙ§ЕуOзїOGЁЭADгкЕуGЃЌ
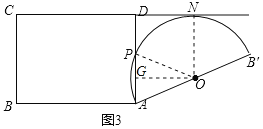
ЁпАыдВгыжБЯпCDЯрЧаЃЌ
ЁрONЁЭDNЃЌ
ЁрЫФБпаЮDGONЮЊОиаЮЃЌ
ЁрDG=ON=2ЃЌ
ЁрAG=AD-DG=1ЃЎ
дкRtЁїAGOжаЃЌЁЯAGO=90ЁуЃЌAO=2ЃЌAG=1ЃЌ
ЁрЁЯAOG=30ЁуЃЌЁЯOAG=60ЁуЃЎ
гжЁпOA=OPЃЌ
ЁрЁїAOPЮЊЕШБпШ§НЧаЮЃЌ
Ёр![]() =
=![]() =
=![]() ІаЃЎ
ІаЃЎ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩжЊЃКЁїAOPЮЊЕШБпШ§НЧаЮЃЌ
ЁрDN=GO=![]() OA=
OA=![]() ЃЌ
ЃЌ
ЁрCN=CD+DN=4+![]() ЃЎ
ЃЎ
ЕБЕуBЁфдкжБЯпCDЩЯЪБЃЌШчЭМ4ЫљЪОЃЌ
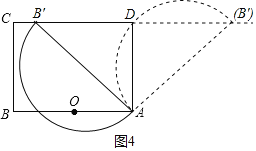
дкRtЁїABЁфDжаЃЈЕуBЁфдкЕуDзѓБпЃЉЃЌABЁф=4ЃЌAD=3ЃЌ
ЁрBЁфD=![]() =
=![]() ЃЌ
ЃЌ
ЁрCBЁф=4-![]() ЃЎ
ЃЎ
ЁпABЁфЮЊжБОЖЃЌ
ЁрЁЯADBЁф=90ЁуЃЌ
ЁрЕБЕуBЁфдкЕуDгвБпЪБЃЌАыдВНЛжБЯпCDгкЕуDЁЂBЁфЃЎ
ЁрЕБАыдВЛЁгыжБЯпCDжЛгавЛИіНЛЕуЪБЃЌ4-![]() ЁмdЃМ4Лђd=4+
ЁмdЃМ4Лђd=4+![]() ЃЎ
ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
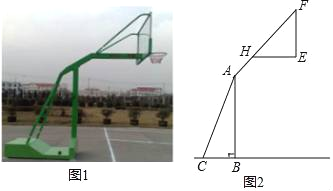
ЁОЬтФПЁПШчЭМ1ЃЌ2ЗжБ№ЪЧФГПюРКЧђМмЕФЪЕЮяЭМгыЪОвтЭМЃЌвбжЊABЁЭBCгкЕуBЃЌЕззљBCЕФГЄЮЊ1УзЃЌЕззљBCгыжЇМмACЫљГЩЕФНЧЁЯACBЃН60ЁуЃЌЕуHдкжЇМмAFЩЯЃЌРКАхЕзВПжЇМмEHЁЮBCЃЌEFЁЭEHгкЕуEЃЌвбжЊAHГЄ![]() УзЃЌHFГЄ
УзЃЌHFГЄ![]() УзЃЌHEГЄ1УзЃЎ
УзЃЌHEГЄ1УзЃЎ
(1)ЧѓРКАхЕзВПжЇМмHEгыжЇМмAFЫљГЩЕФНЧЁЯFHEЕФЖШЪ§ЃЎ
(2)ЧѓРКАхЕзВПЕуEЕНЕиУцЕФОрРыЃЎ(НсЙћБЃСєИљКХ)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
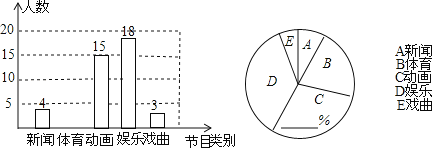
ЁОЬтФПЁПШчЭМЃЌЕШбќШ§НЧаЮABCЕФЕзБпBCГЄЮЊ4ЃЌУцЛ§ЪЧ16ЃЌбќACЕФДЙжБЦНЗжЯпEFЗжБ№НЛACЃЌABБпгкEЃЌFЕу![]() ШєЕуDЮЊBCБпЕФжаЕуЃЌЕуMЮЊЯпЖЮEFЩЯвЛЖЏЕуЃЌдђ
ШєЕуDЮЊBCБпЕФжаЕуЃЌЕуMЮЊЯпЖЮEFЩЯвЛЖЏЕуЃЌдђ![]() жмГЄЕФзюаЁжЕЮЊ
жмГЄЕФзюаЁжЕЮЊ![]() ЁЁЁЁ
ЁЁЁЁ![]()

A. 6 B. 8 C. 10 D. 12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫСЫНтбЇЩњЖдаТЮХЁЂЬхг§ЁЂЖЏЛЁЂгщРжЁЂЯЗЧњЮхРрЕчЪгНкФПЕФЯВАЎЧщПіЃЌЫцЛњГщШЁСЫБОаЃВПЗжбЇЩњНјааЮЪОэЕїВщЃЈБибЁЧвжЛбЁвЛРрНкФПЃЉЃЌНЋЕїВщНсЙћНјааећРэКѓЃЌЛцжЦСЫШчЯТВЛЭъећЕФЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЌЦфжаЯВАЎЬхг§НкФПЕФбЇЩњШЫЪ§БШЯВАЎЯЗЧњНкФПЕФбЇЩњШЫЪ§ЕФ3БЖЛЙЖр1ШЫЃЎ
ЧыИљОнЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓБОДЮГщШЁЕФбЇЩњШЫЪ§ЃЎ
ЃЈ2ЃЉВЙШЋЬѕаЮЭМЃЌдкЩШаЮЭГМЦЭМжаЕФКсЯпЩЯЬюЩЯе§ШЗЕФЪ§жЕЃЌВЂжБНгаДГіЁАЬхг§ЁБЖдгІЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЎ
ЃЈ3ЃЉИУаЃга3000УћбЇЩњЃЌЧѓИУаЃЯВАЎгщРжНкФПЕФбЇЩњДѓдМгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌЪ§жсЩЯШ§ИіЕуAЁЂOЁЂPЃЌЕуOЪЧдЕуЃЌЙЬЖЈВЛЖЏЃЌЕуAКЭBПЩвдвЦЖЏЃЌЕуAБэЪОЕФЪ§ЮЊ![]() ЃЌЕуBБэЪОЕФЪ§ЮЊ
ЃЌЕуBБэЪОЕФЪ§ЮЊ![]() .
.
ЃЈ1ЃЉШєAЁЂBвЦЖЏЕНШчЭМЫљЪОЮЛжУЃЌМЦЫу![]() ЕФжЕ.
ЕФжЕ.
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЧщПіЯТЃЌBЕуВЛЖЏЃЌЕуAЯђзѓвЦЖЏ3ИіЕЅЮЛГЄЃЌаДГіAЕуЖдгІЕФЪ§![]() ЃЌВЂМЦЫу
ЃЌВЂМЦЫу![]() .
.
ЃЈ3ЃЉдкЃЈ1ЃЉЕФЧщПіЯТЃЌЕуAВЛЖЏЃЌЕуBЯђгввЦЖЏ15.3ИіЕЅЮЛГЄЃЌДЫЪБ![]() БШ
БШ![]() ДѓЖрЩйЃПЧыСаЪНМЦЫу.
ДѓЖрЩйЃПЧыСаЪНМЦЫу.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМУФЯФГжабЇдкВЮМгЁАДДЮФУїГЧЃЌЕудоШЊГЧЁБЪщЛБШШќжаЃЌбюРЯЪІДгШЋаЃ30ИіАржаЫцЛњГщШЁСЫ4ИіАрЃЈгУAЃЌBЃЌCЃЌDБэЪОЃЉЃЌЖдеїМЏЕНЕФзїЖІЕФЪ§СПНјааСЫЗжЮіЭГМЦЃЌжЦзїСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЎ

ЧыИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈlЃЉбюРЯЪІВЩгУЕФЕїВщЗНЪНЪЧЁЁ ЁЁЃЈЬюЁАЦеВщЁБЛђЁАГщбљЕїВщЁБЃЉЃЛ
ЃЈ2ЃЉЧыВЙГфЭъећЬѕаЮЭГМЦЭМЃЌВЂМЦЫуЩШаЮЭГМЦЭМжаCАрзїЦЗЪ§СПЫљЖдгІЕФдВаФНЧЖШЪ§ЁЁ ЁЁЃЎ
ЃЈ3ЃЉЧыЙРМЦШЋаЃЙВеїМЏзїЦЗЕФЪВЪ§ЃЎ
ЃЈ4ЃЉШчЙћШЋжІеїМЏЕФзїЦЗжага5МўЛёЕУвЛЕШНБЃЌЦфжага3УћзїепЪЧФаЩњЃЌ2УћзїепЪЧХЎЩњЃЌЯжвЊдкЛёЕУвЛбљЕШНБЕФзїепжабЁШЁСНШЫВЮМгБэеУзљЬИЛсЃЌЧыФугУСаБэЛђЪїзДЭМЕФЗНЗЈЃЌЧѓЧЁКУбЁШЁЕФСНУћбЇЩњадБ№ЯрЭЌЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
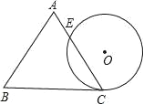
ЁОЬтФПЁПвЛИіБпГЄЮЊ 4cm ЕФЕШБпШ§НЧаЮ ABC гыЁбO ЕШИпЃЌ ШчЭМЗХжУЃЌЁбO гы BC ЯрЧагкЕу CЃЌЁбO гы AC ЯрНЛгкЕуEЃЌдђ CE ЕФГЄЮЊ _____cmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
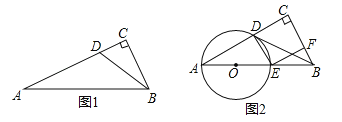
ЁОЬтФПЁПШчЭМ1ЃЌRtЁїACB жаЃЌЁЯC=90ЁуЃЌЕуDдкACЩЯЃЌЁЯCBD=ЁЯAЃЌЙ§AЁЂDСНЕуЕФдВЕФдВаФOдкABЩЯЃЎ
ЃЈ1ЃЉРћгУжБГпКЭдВЙцдкЭМ1жаЛГіЁбOЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЌВЂгУКкЩЋЫЎБЪАбЯпЬѕУшЧхГўЃЉЃЛ
ЃЈ2ЃЉХаЖЯBDЫљдкжБЯпгыЃЈ1ЃЉжаЫљзїЕФЁбOЕФЮЛжУЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЛ
ЃЈ3ЃЉЩшЁбOНЛABгкЕуEЃЌСЌНгDEЃЌЙ§ЕуEзїEFЁЭBCЃЌFЮЊДЙзуЃЌШєЕуDЪЧЯпЖЮACЕФЛЦН№ЗжИюЕуЃЈМД![]() ЃЉЃЌШчЭМ2ЃЌЪдЫЕУїЫФБпаЮDEFCЪЧе§ЗНаЮЃЎ
ЃЉЃЌШчЭМ2ЃЌЪдЫЕУїЫФБпаЮDEFCЪЧе§ЗНаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
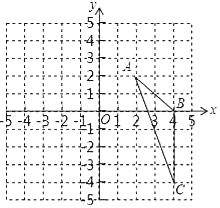
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїABCШ§ИіЖЅЕуЕФзјБъЗжБ№ЪЧAЃЈ2ЃЌ2ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ4ЃЌЉ4ЃЉЃЎ
ЃЈ1ЃЉЧыдкЭМжаЃЌЛГіЁїABCЯђзѓЦНвЦ6ИіЕЅЮЛГЄЖШКѓЕУЕНЕФЁїA1B1C1ЃЛ
ЃЈ2ЃЉвдЕуOЮЊЮЛЫЦжааФЃЌНЋЁїABCЫѕаЁЮЊдРДЕФ![]() ЃЌЕУЕНЁїA2B2C2ЃЌЧыдкЭМжаyжсгвВрЃЌЛГіЁїA2B2C2ЃЌВЂЧѓГіЁЯA2C2B2ЕФе§ЯвжЕЃЎ
ЃЌЕУЕНЁїA2B2C2ЃЌЧыдкЭМжаyжсгвВрЃЌЛГіЁїA2B2C2ЃЌВЂЧѓГіЁЯA2C2B2ЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com