
 如图,菱形ABCD的周长为16,若∠BAD=60°,E是AB的中点,则点E的坐标为($\sqrt{3}$,1).
如图,菱形ABCD的周长为16,若∠BAD=60°,E是AB的中点,则点E的坐标为($\sqrt{3}$,1). 分析 首先求出AB的长,进而得出EO的长,再利用锐角三角函数关系求出E点横纵坐标即可.
解答 解:过E作EM⊥AC,EN⊥BD,
∵四边形ABCD是菱形,
∴AB=CD=BC=AD,AC⊥DB,∠BAO=$\frac{1}{2}$∠BAD,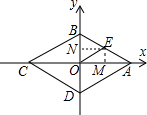
∵∠BAD=60°,
∴∠BAO=30°,
∵AC⊥DB,
∴∠BOA=90°,
∵E是AB的中点,
∴EO=EA=EB=$\frac{1}{2}$AB,
∵菱形ABCD的周长为16,
∴AB=4,
∴EO=2,
∵EO=AE,
∴∠EOA=∠EAO=30°,
∴EM=1,
∵∠EOA=30°,∠BOA=90°,
∴∠BOE=60°,
∴EN=EO•sin60°=$\sqrt{3}$,
∴则点E的坐标为:($\sqrt{3}$,1).
故答案为($\sqrt{3}$,1).
点评 此题主要考查了菱形的性质以及锐角三角函数关系应用,根据已知得出EO的长以及∠EOA=∠EAO=30°是解题关键.


科目:初中数学 来源: 题型:选择题
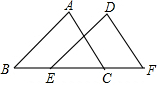 如图所示,△DEF是由△ABC经过平移得到的,则平移的距离可能是( )
如图所示,△DEF是由△ABC经过平移得到的,则平移的距离可能是( )| A. | 线段BC的长度 | B. | 线段EC的长度 | C. | 线段BE的长度 | D. | 线段BF的长度 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一组对边平行且相等,一个角是直角 | |
| B. | 对角线互相平分且相等 | |
| C. | 有三个角是直角 | |
| D. | 一组对边平行,另一组对边相等,且对角线相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式( )
如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式( )| A. | y=2x-5 | B. | y=2x2+7 | C. | y=$\frac{1}{x(x+1)}$ | D. | y=$\sqrt{x+2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )| A. | (1,3) | B. | (3,2) | C. | (0,3) | D. | (-3,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com