考点:一次函数图象上点的坐标特征,相似三角形的判定与性质
专题:规律型
分析:根据图象上点的坐标性质得出点B1、B2、B3、…、Bn、Bn+1各点坐标,进而利用相似三角形的判定与性质得出S1、S2、S3、…、Sn,进而得出答案.
解答:解:∵A
1、A
2、A
3、…、A
n、A
n+1是x轴上的点,且OA
1=A
1A
2=A
2A
3=…=A
nA
n+1=1,
分别过点A
1、A
2、A
3、…、A
n、A
n+1作x轴的垂线交直线y=2x于点B
1、B
2、B
3、…、B
n、B
n+1,
∴B
1的横坐标为:1,纵坐标为:2,
∴B
1(1,2),
同理可得:B
2的横坐标为:2,纵坐标为:4,
则B
2(2,4),
B
3(2,6)…
∵A
1B
1∥A
2B
2,
∴△A
1B
1P
1∽△A
2B
2P
1,
∴
=
,
∴△A
1B
1C
1与△A
2B
2C
2对应高的比为:1:2,
∴A
1B
1边上的高为:
,
∴S
△A1B1P1=
×
×2=3,
同理可得出:S
△A2B2P2=
,S
△A3B3P3=
,
∴S
n=
.
故答案为:
.
点评:此题考查了一次函数函数图象上点的坐标特点,先根据题意得出B点坐标变化规律进而得出S的变化规律,得出图形面积变化规律是解题关键.

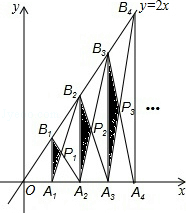
 如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…
如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…

