
【题目】如图,已知二次函数y=ax2+bx+c(a,b,c为常数)的对称轴为x=1,与y轴的交点为c(0,4),y的最大值为5,顶点为M,过点D(0,1)且平行于x轴的直线与抛物线交于点A,B.
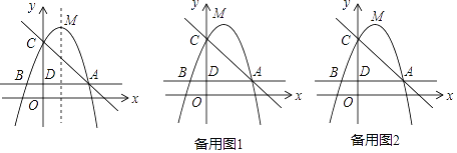
(Ⅰ)求该二次函数的解析式和点A、B的坐标;
(Ⅱ)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,求出所有点P的坐标.
【答案】(Ⅰ)y=﹣x2+2x+4,B(﹣1,1),A(3,1);(Ⅱ)P点坐标为(3,1)或(﹣3,7)或(![]() )或(
)或(![]() ).
).
【解析】
(Ⅰ)先确定顶点M的坐标,再设顶点式y=a(x﹣1)2+5,然后把C点坐标代入求出a即可得到抛物线解析式;在计算函数值为1所对应的自变量的值即可得到A、B点的坐标;
(Ⅱ)先计算出CD=3,BD=1,AM=2![]() ,CM
,CM![]() ,AC=3
,AC=3![]() ,则利用勾股定理的逆定理得到△ACM为直角三角形,∠ACM=90°,然后分两种情况讨论:①当
,则利用勾股定理的逆定理得到△ACM为直角三角形,∠ACM=90°,然后分两种情况讨论:①当![]() 时,△MCP∽△BDC,即
时,△MCP∽△BDC,即![]() ,解得PC=3
,解得PC=3![]() ,设此时P(x,﹣x+4),利用两点间的距离公式得到x2+(﹣x+4﹣4)2=(3
,设此时P(x,﹣x+4),利用两点间的距离公式得到x2+(﹣x+4﹣4)2=(3![]() )2,求出x从而得到此时P点坐标;
)2,求出x从而得到此时P点坐标;
②当![]() 时,△MCP∽△CDB,即
时,△MCP∽△CDB,即![]() ,解得PC
,解得PC![]() ,利用同样方法求出对应的P点坐标.
,利用同样方法求出对应的P点坐标.
(Ⅰ)根据题意得抛物线的顶点M的坐标为(1,5),设抛物线的解析式为y=a(x﹣1)2+5,把C(0,4)代入y=a(x﹣1)2+5得:a+5=4,解得:a=﹣1,所以抛物线解析式为y=﹣(x﹣1)2+5,即y=﹣x2+2x+4;
当y=1时,﹣x2+2x+4=1,解得:x1=﹣1,x2=3,则B(﹣1,1),A(3,1);
(Ⅱ)CD=3,BD=1,AM![]()
![]() ,CM
,CM![]() ,易得直线AC的解析式为y=﹣x+4.
,易得直线AC的解析式为y=﹣x+4.
∵CM2+AC2=AM2,∴△ACM为直角三角形,∠ACM=90°,∴∠BDC=∠MCP,分两种情况讨论:
①当![]() 时,△MCP∽△BDC,即
时,△MCP∽△BDC,即![]() ,解得:PC=3
,解得:PC=3![]() ,设此时P(x,﹣x+4),∴x2+(﹣x+4﹣4)2=(3
,设此时P(x,﹣x+4),∴x2+(﹣x+4﹣4)2=(3![]() )2,解得:x=±3,则此时P点坐标为(3,1)或(﹣3,7);
)2,解得:x=±3,则此时P点坐标为(3,1)或(﹣3,7);
②当![]() 时,△MCP∽△CDB,即
时,△MCP∽△CDB,即![]() ,解得:PC
,解得:PC![]() ,设此时P(x,﹣x+4),∴x2+(﹣x+4﹣4)2=(
,设此时P(x,﹣x+4),∴x2+(﹣x+4﹣4)2=(![]() )2,解得:x=±
)2,解得:x=±![]() ,则此时P点坐标为(
,则此时P点坐标为(![]() )或(
)或(![]() );
);
综上所述:满足条件的P点坐标为(3,1)或(﹣3,7)或(![]() )或(
)或(![]() ).
).


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】如图,把一副三角板如图①放置,其中,∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图②).
(1)求∠OFE1的度数;
(2)求线段AD1的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积.
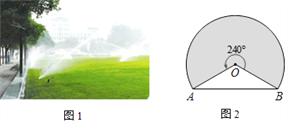
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=![]() ﹣2x的图象与性质.
﹣2x的图象与性质.
小东根据学习函数的经验,对函数y=![]() ﹣2x的图象与性质进行了探究.
﹣2x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=![]() ﹣2x的自变量x的取值范围是_______;
﹣2x的自变量x的取值范围是_______;
(2)如表是y与x的几组对应值
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | m |
|
| … |
则m的值为_______;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)观察图象,写出该函数的两条性质________.
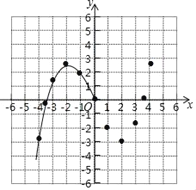
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P(如图2),则六边形AEFCHG面积的最大值是( )

A. ![]() B.
B. ![]() C. 2﹣
C. 2﹣ ![]() D. 1+
D. 1+ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折到△AFE,延长EF交边BC于点G,连接AG,CF,下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S![]() =
=![]() ,其中正确的有( )个.
,其中正确的有( )个.
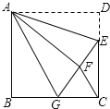
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△CDE的顶点C点坐标为C(1,﹣2),点D的横坐标为![]() ,将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.
,将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.
(1)图中,∠OCE等于∠_____;
(2)求抛物线的解析式;
(3)抛物线上是否存在点P,使S△PAE=![]() S△CDE?若存在,直接写出点P的坐标;若不存在,请说明理由.
S△CDE?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com