
【题目】如图,把一副三角板如图①放置,其中,∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图②).
(1)求∠OFE1的度数;
(2)求线段AD1的长.

【答案】(1)120°;(2)5.
【解析】
(1)利用已知得出∠BCO=45°,进而根据三角形内角和定理求出∠BOC的度数;
(2)根据OFE1=∠B+∠1,易得∠OFE1的度数,进而得出∠4=90°,在Rt△AD1O中根据勾股定理就可以求得AD1的长.
(1)如图乙所示,
∠BCO=60°-15°=45°,
∠BOC=180°-45°-45°=90°;
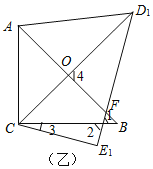
(2)如图乙所示,
∵∠3=15°,∠E1=90°,
∴∠1=∠2=75°,
又∵∠B=45°,
∴∠OFE1=∠B+∠1=45°+75°=120°;
∴∠D1FO=60°,
∵∠CD1E1=30°,
∴∠4=90°,
又∵AC=BC,∠A=45°
即△ABC是等腰直角三角形.
∴OA=OB=![]() AB=3cm,
AB=3cm,
∵∠ACB=90°,
∴CO=![]() AB=
AB=![]() ×6=3(cm),
×6=3(cm),
又∵CD1=7(cm),
∴OD1=CD1-OC=7-3=4(cm),
在Rt△AD1O中,AD1=![]() (cm)
(cm)


科目:初中数学 来源: 题型:
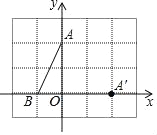
【题目】如图,在平面直角坐标系xOy中,点A,点B的坐标分别为(0,2),(-1,0),将△ABO绕点O顺时针旋转,若点A的对应点A′的坐标为(2,0),
(1)则点B的对应点B′的坐标为_____;
(2)画出旋转后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的是_________(只填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
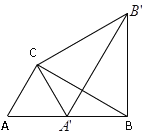
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,AC=2cm.现在将△ABC绕点C逆时针旋转至△A′B′C′,使得点A′恰好落在AB上,连接BB′,则BB′的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
【答案】y=﹣5x2+2x﹣1
【解析】试题分析:根据二次函数的定义得到m2+m﹣4=2且m﹣2≠0,由此求得m的值,进而得到该二次函数的解析式.
试题解析:依题意得:m2+m﹣4=2且m﹣2≠0. 即(m﹣2)(m+3)=0且m﹣2≠0,
解得m=﹣3,
则该二次函数的解析式为y=﹣5x2+2x﹣1
【题型】解答题
【结束】
21
【题目】如图,在ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 |
摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
摸到黑球的频率 |
|
|
|
| a |
![]() 表中a的值等于______;
表中a的值等于______;
![]() 估算口袋中白球的个数;
估算口袋中白球的个数;
![]() 用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a,b,c为常数)的对称轴为x=1,与y轴的交点为c(0,4),y的最大值为5,顶点为M,过点D(0,1)且平行于x轴的直线与抛物线交于点A,B.
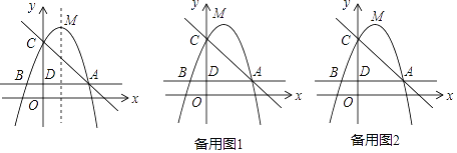
(Ⅰ)求该二次函数的解析式和点A、B的坐标;
(Ⅱ)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,求出所有点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com