
����Ŀ����֪����y=��m��2��xm2+m-4 +2x��1��һ�����κ�������ö��κ����Ľ���ʽ��
���𰸡�y=��5x2+2x��1
��������������������ݶ��κ����Ķ���õ�m2+m��4=2��m��2��0���ɴ����m��ֵ�������õ��ö��κ����Ľ���ʽ��
���������������ã�m2+m��4=2��m��2��0�� ����m��2����m+3��=0��m��2��0��
���m=��3��
��ö��κ����Ľ���ʽΪy=��5x2+2x��1
�����͡������
��������
21
����Ŀ����ͼ����ABCD�У�EF��AB��FG��ED��DE��DA=2��5��EF=4�����߶�CG�ij���


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̼���1200Ԫ������һ��T�������к�ܿ����꣬�̼�����2800Ԫ�����˵ڶ�������T�������������ǵ�һ����������2���������۹���5Ԫ��
��1�����̼ҹ����ĵ�һ��T���Ƕ��ټ���
��2��������T������ͬ�ı�����ۣ����ʣ��20���������Ż����������ϣ������T��ȫ������������ʲ�����16%���������������أ�����ôÿ��T���ı�������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABCƽ�ƺ�ó���A1B1C1����A����1��3��ƽ�ƺ��A1����4��2��������֪B1����2��3����C1��1����1������B��C���꣬��ͼ��˵��������������ƽ�ƣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ļ���һ�죬����Ϊ1.6m��С�������һ����ǰ�����ĸ߶ȣ���������ӰBA��B��A��ȥ�����ߵ�C��ʱ������Ӱ�Ӷ�������������Ӱ�Ӷ����غϣ����BC=3.2m��CA=0.8m�����ǵó����ĸ߶�Ϊ(����)

A��8m B��6.4m C��4.8m D��10m
���𰸡�A.
��������
�����������Ϊ�˺�������ֱ�ڵ��棬���Ժ��߹��ɵ�����ֱ�����������ƣ�
������x�ף���![]() ����
����![]() ����ã�x=8. ��ѡA.
����ã�x=8. ��ѡA.
���㣺���������ε�Ӧ��.
�����͡���ѡ��
��������
11
����Ŀ����֪Բ�ĵ���뾶Ϊ1cm��ĸ�߳�Ϊ3cm������ȫ���Ϊ________cm2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������������̣�
��ͼ��ʾ����E��![]() �ⲿ����D��BC���ϣ�DE��AC��F����
�ⲿ����D��BC���ϣ�DE��AC��F����![]() ��
��![]() ��
��
��֤��![]() ��
��

֤������![]() ����֪����
����֪����
![]() ��________________����
��________________����
��![]() ��________________����
��________________����
�֡�![]() ��
��
��________![]() ________
________![]() ��________����
��________����
��![]() ��
��
��![]() ��
��![]() ��
��
![]() ����֤��
����֤��
��![]() ����֪��
����֪��
![]() ����֤��
����֤��
��![]() ��________��.
��________��.
��![]() ��________________��
��________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ��ֱ
��ֱ![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��
��1����ϸ�۲�ͼ�Σ�ֱ��д��![]() ��
��
��2����![]() ��
��![]() ��ֵ��
��ֵ��
��3���ڷ���������ͼ�����Ƿ���ڵ�![]() ��ʹ�ı���
��ʹ�ı���![]() Ϊƽ���ı��Σ�������ڣ������
Ϊƽ���ı��Σ�������ڣ������![]() �����꣬��������ڣ���˵�����ɣ�
�����꣬��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
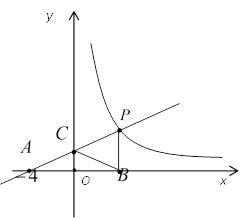
����Ŀ����ͼ����ֱ��y=![]() x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
��1����������F1����ʾ�Ķ��κ����ı���ʽ��
��2������M��������F1λ�ڵڶ�����ͼ���ϵ�һ�㣬���ı���MAOC����BOC������ֱ�ΪS�ı���MAOC��S��BOC����S=S�ı���MAOC��S��BOC����S���ʱ��M�����꼰S�����ֵ��
��3����ͼ������������F1��y�ᷭ�۲����������õ�������F2����A��B�루2��������ĵ�M�Ķ�Ӧ��ֱ�ΪA����B����M��������M����M��E��x���ڵ�E����ֱ��A��C�ڵ�D����x�����Ƿ���ڵ�P��ʹ����A����D��PΪ���������������AB��C���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O�ڵ�B��OA����O��C�㣬��C��DC��OA��AB��D����BD��AD=1��2��
��1������A������ֵ��
��2����OC=1����AB��![]() �ij���
�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=90������ABC=32�����Ե�CΪ��ת����˳ʱ����ת��õ���A��B��C���ҵ�A�ڱ�A��B���ϣ�����ת�ǵĶ���Ϊ______��
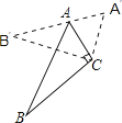
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com