
����Ŀ����ͼ����ֱ��y=![]() x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
��1����������F1����ʾ�Ķ��κ����ı���ʽ��
��2������M��������F1λ�ڵڶ�����ͼ���ϵ�һ�㣬���ı���MAOC����BOC������ֱ�ΪS�ı���MAOC��S��BOC����S=S�ı���MAOC��S��BOC����S���ʱ��M�����꼰S�����ֵ��
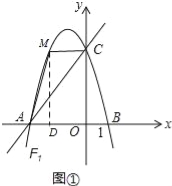
��3����ͼ������������F1��y�ᷭ�۲����������õ�������F2����A��B�루2��������ĵ�M�Ķ�Ӧ��ֱ�ΪA����B����M��������M����M��E��x���ڵ�E����ֱ��A��C�ڵ�D����x�����Ƿ���ڵ�P��ʹ����A����D��PΪ���������������AB��C���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() x2��
x2��![]() x+4����2�����ֵΪ
x+4����2�����ֵΪ![]() ��M����
��M����![]() ��5������3����2��0������
��5������3����2��0������![]() ��0��
��0��
��������
�����������1������һ�κ����Ľ���ʽ�����A��C�����꣬Ȼ��������B�����꼴��������κ����Ľ���ʽ����2������M��������F1�ϣ����Կ���M��a����![]() a2��
a2��![]() a+4����Ȼ��ֱ����S�ı���MAOC��S��BOC������M��MD��x���ڵ�D����S�ı���MAOC��ֵ������ADM�����������DOCM�����֮�ͣ���3������û��˵����P�ľ���λ�ã�������Ҫ����P��λ�ý��з������ۣ�����P��A�����ұ�ʱ��������Dz����ڣ�����P��A�������ʱ����ʱ��DA��P=��CAB��������A����D��PΪ���������������AB��C���ƣ����Ϊ������������������ۣ���
a+4����Ȼ��ֱ����S�ı���MAOC��S��BOC������M��MD��x���ڵ�D����S�ı���MAOC��ֵ������ADM�����������DOCM�����֮�ͣ���3������û��˵����P�ľ���λ�ã�������Ҫ����P��λ�ý��з������ۣ�����P��A�����ұ�ʱ��������Dz����ڣ�����P��A�������ʱ����ʱ��DA��P=��CAB��������A����D��PΪ���������������AB��C���ƣ����Ϊ������������������ۣ���![]() =
=![]() ����
����![]() =
=![]() ��
��
����������⣺��1����y=0����y=![]() x+4��
x+4��
��x=��3��
A����3��0����
��x=0������y=![]() x+4��
x+4��
��y=4��
��C��0��4����
��������F1�Ľ���ʽΪ��y=a��x+3����x��1����
��C��0��4��������ʽ�ã�a=��![]() ��
��
��y=��![]() x2��
x2��![]() x+4��
x+4��
��2����ͼ�������M��a����![]() a2��
a2��![]() a+4��
a+4��
������3��a��0
��B��1��0����C��0��4����
��OB=1��OC=4
��S��BOC=![]() OBOC=2��
OBOC=2��
����M��MP��x���ڵ�P��
��MP=��![]() a2��
a2��![]() a+4��AP=a+3��OP=��a��
a+4��AP=a+3��OP=��a��
��S�ı���MAOC=![]() APMP+
APMP+![]() ��MP+OC��OP
��MP+OC��OP
=![]() APMP+
APMP+![]() OPMP+
OPMP+![]() OPOC
OPOC
=![]() +
+![]()
=![]() +
+![]()
=![]() ��3����
��3����![]() a2��
a2��![]() a+4��+
a+4��+![]() ��4������a��
��4������a��
=��2a2��6a+6
��S=S�ı���MAOC��S��BOC
=����2a2��6a+6����2
=��2a2��6a+4
=��2��a+![]() ��2+
��2+![]()
����a=��![]() ʱ��
ʱ��
S�����ֵ�����ֵΪ![]()
��ʱ��M����![]() ��5����
��5����
��3����ͼ����������֪��M����![]() ����
����
��AB��=2��
��ֱ��A��C�Ľ���ʽΪ��y=kx+b��
��A����3��0����C��0��4������y=kx+b��
�ã�![]() ��
��
��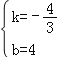
��y=��![]() x+4��
x+4��
��x=![]() ����y=��
����y=��![]() x+4��
x+4��
��y=2
��![]()
�ɹ��ɶ����ֱ����ã�AC=5��DA��=![]()
��P��m��0��
��m��3ʱ��
��ʱ��P��A������ߣ�
���DA��P=��CAB����
��![]() =
=![]() ʱ����DA��P�ס�CAB����
ʱ����DA��P�ס�CAB����
��ʱ��![]() =
=![]() ��3��m����
��3��m����
��ã�m=2��
��P��2��0��
��![]() =
=![]() ʱ����DA��P�ס�B��AC��
ʱ����DA��P�ס�B��AC��
��ʱ��![]() =
=![]() ��3��m��
��3��m��
m=��![]() ��
��
��P����![]() ��0��
��0��
��m��3ʱ��
��ʱ����P��A���ұߣ�
������CB��O�١�DA��E��
���AB��C�١�DA��P
�����������DA��P����B��AC�������ƣ�
��������������A����D��PΪ���������������AB��C����ʱ����P������Ϊ��2��0������![]() ��0����
��0����


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ƶ�C˳ʱ����ת90���õ�����FGCE����M��N�ֱ���BD��GE���е㣬��BC=14��CE=2����MN�ij���������

A. 7 B. 8 C. 9 D. 10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��3��y1����B��4��y2������������y=x2+1�ϣ��ԱȽ�y1��y2�Ĵ�С��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A(��2��1)�ڣ� ��
A. ��һ���� B. �ڶ����� C. �������� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ����
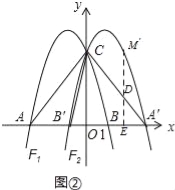
��ͼ�٣����ı���ADBC�У���ACB=��ADB=90�㣬AD=BD��̽���߶�AC��BC��CD֮���������ϵ��
С��ͬѧ̽���������˼·�ǣ�����BCD�Ƶ�D����ʱ����ת90�㵽��AED������B��C�ֱ����ڵ�A��E������ͼ�ڣ�����֤��C��A��E��ͬһ��ֱ���ϣ����ҡ�CDE�ǵ���ֱ�������Σ�����CE=![]() CD���Ӷ��ó����ۣ�AC+BC=
CD���Ӷ��ó����ۣ�AC+BC=![]() CD��
CD��
��Ӧ�ã�
��1����ͼ���У���AC=![]() ��BC=
��BC=![]() ����CD= ��
����CD= ��
��2����ͼ�ۣ�AB�ǡ�O��ֱ������C��D�ڡ��ϣ�![]() ����AB=13��BC=12����CD�ij���
����AB=13��BC=12����CD�ij���
��չ���ɣ�
��3����ͼ�ܣ���ACB=��ADB=90�㣬AD=BD����AC=m��BC=n��m��n������CD�ij����ú�m��n�Ĵ���ʽ��ʾ��
��4����ͼ�ݣ���ACB=90�㣬AC=BC����PΪAB���е㣬����E����AE=![]() AC��CE=CA����QΪAE���е㣬���߶�PQ��AC��������ϵ�� ��
AC��CE=CA����QΪAE���е㣬���߶�PQ��AC��������ϵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ�˽�ij�о��꼶ѧ��������״�������г����500��ѧ��������״������ô������ָ�� ��
A. ij�����еľ��꼶ѧ��
B. ������500�����꼶ѧ��
C. ij�����еľ��꼶ѧ��������״��
D. ������500��ѧ��������״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н�����������Ϊ���˽����꼶ѧ��ÿѧ�ڲμ��ۺ�ʵ�����������������������ijУ��ѧ��һ��ѧ�ڲμ��ۺ�ʵ��������������õõ������ݻ�������ͼ������������ͳ��ͼ��
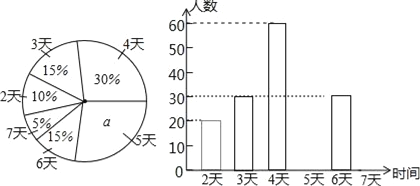
�������ͼ���ṩ����Ϣ���ش��������⣺
��1���������ͳ��ͼ�е�a��ֵ���������У���꼶ѧ��������
��2���ֱ�����ʱ��Ϊ5�졢7���ѧ������������ȫƵ���ֲ�ֱ��ͼ��
��3���������ͳ��ͼ�С��ʱ��Ϊ4�족����������Բ�ĽǵĶ�����
��4��������й������꼶ѧ��6000�ˣ�������ơ��ʱ�䲻С��4�족�Ĵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�A��B��C���������ֱ�Ϊ����6��7��������3��0������0��3����
��1��������ABC��������ABC�������
��2������ABC�У���C����ƽ�ƺ�Ķ�Ӧ��ΪC�䣨5��4��������ABC��ͬ����ƽ�Ƶõ���A��B��C�䣬 ����ƽ�ƺ����A��B��C������д����A�䣬B�������ꣻ
��3����֪��P����3��m��Ϊ��ABC��һ�㣬����P����ƽ��4����λ��������ƽ��6����λ�õ���Q��n����3������m=���� ����n=���� �� ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com